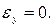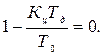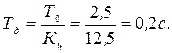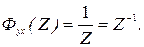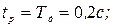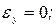Постановка задачи синтеза цифровой системы автоматического управления
Задача синтеза цифровой системы автоматического управления может быть сформулирована следующим образом: известны характеристики закона управления, заданы требования к системе управления и система управления, необходимо выбрать закон управления и значения его коэффициентов. В общем случае при синтезе необходимо учитывать противоречивое влияние различных факторов, противоречивость отдельных характеристик системы, поэтому требования к системе могут быть сформулированы в виде экстремального значения заданного критерия. Таким образом, в этом случае синтез состоит в определении оптимального закона управления (оптимальной системы), обеспечивающего экстремум заданного критерия. При недостоверно известных характеристиках объекта управления приходится решать задачу выбора адаптивных законов управления. Рассмотрим одну из простейших задач синтеза системы, которую разделим на два этапа: 1.Выбор закона управления из числа типовых, 2. Выбор параметров (коэффициентов), обеспечивающих совокупность требований. Пример. Задание. 1.Объект управления задан передаточной функцией
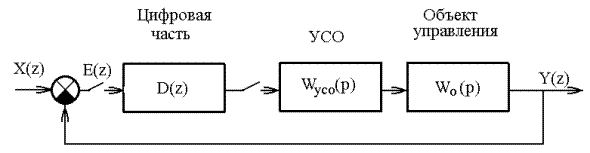
2. Устройство связи объекта управления с цифровой связью – фиксирующее звено нулевого порядка. 3. Выбрать закон управления и его коэффициенты из условия точности по заданию: а) б) 4. Оценить качество системы при выбранных характеристиках регулятора. 5. Определить период дискретности из условия затухания процесса за один период дискретности. Решение. 1. Составим структурную схему автоматического управления.
2. Определим эквивалентную Z-передаточную функцию объекта управления и устройства связи цифровой части с объектом управления
Так как знаменатель передаточной функции содержит единичный положительный корень, заданная точность обеспечивается пропорциональным законом управления. Передаточная функция цифровой части системы
Передаточная функция разомкнутой системы
4. Определим коэффициент усиления цифровой части системы, исходя из заданной динамической точности:
5. Строим область устойчивости для параметров Характеристическое уравнение замкнутой системы
Условие устойчивости, чтобы корень характеристического уравнения по модулю был бы меньше 1.
Уравнение для границы устойчивости
Отсюда получаем связь между
Граница устойчивости, а также определенная по условию устойчивости область устойчивости представлены на рисунке
Предельное значение периода дискретности, определенное по области устойчивости, или аналитически
6. Выбираем из условия обеспечения определенного запаса период дискретности
Для оценки качества управления строим переходную характеристику. Передаточная функция замкнутой системы
Преобразуем передаточную функцию замкнутой системы к виду:
Отсюда рекуррентное уравнение для определения переходной функции:
при начальных условиях
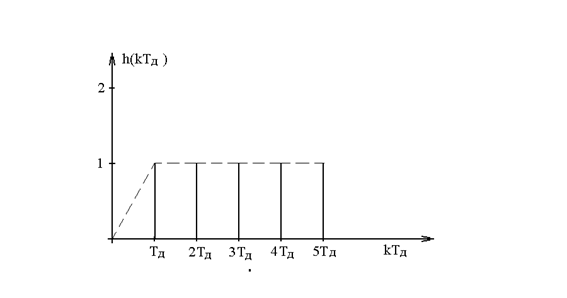
График переходной функции представлен на рисунке
Система управления характеризуется следующим качеством: а) перерегулирование б) время регулирования в) установившаяся ошибка 8. Переходный процесс затухает за один период дискретности, если в знаменателе передаточной функции имеется один нулевой корень. Условие получения одного нулевого корня
Отсюда период дискретности
При этом передаточная функция принимает вид:
Рекуррентное уравнение для определения переходной функции
График переходной функции представлен на рисунке
Качественные показатели системы управления следующие: а) перерегулирование б) время регулирования в) установившаяся ошибка Таким образом, в цифровых системах управления требуемое качество управления может быть обеспечено не только путем выбора соответствующих настроек регулятора, но и путем изменения периода дискретности.
|

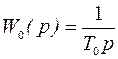 ;
; 
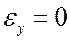 при
при  ;
;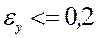 при
при 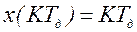 ;
;
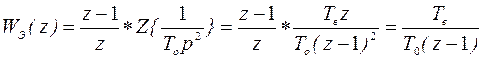
 3. Выбираем вид закона управления, исходя из статической точности ey=0.
3. Выбираем вид закона управления, исходя из статической точности ey=0.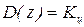
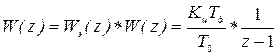


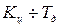 для того, чтобы определить период дискретности
для того, чтобы определить период дискретности 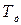 .
.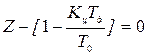

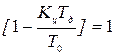
 и
и  :
:


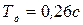
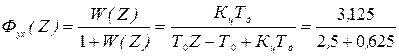
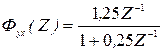
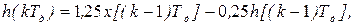

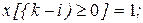
 .
.