Пусть X - дискретная случайная величина, которая при выборке объемом n получила значения  . Допустим, что известен вид закона распределения вероятностей, но неизвестен параметр
. Допустим, что известен вид закона распределения вероятностей, но неизвестен параметр 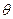 .
.
Обозначим через 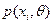 вероятность того, что величина X принимает значения
вероятность того, что величина X принимает значения 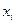 ,
, 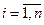 . Функцией правдоподобия дискретной случайной величины называют функцию
. Функцией правдоподобия дискретной случайной величины называют функцию
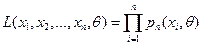 (54.1)
(54.1)
Точечной оценкой параметра 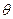 считается такое значение
считается такое значение 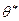 , при котором функция L принимает наибольшее значение. Эту оценку называют оценкой наибольшего правдоподобия.
, при котором функция L принимает наибольшее значение. Эту оценку называют оценкой наибольшего правдоподобия.
Так как функции L и lnL обычно принимают наибольшее значение при одном и том же 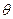 , то оценку
, то оценку 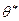 определяют на основе максимизации функции lnL. Для этого функцию исследуют на максимум с помощью необходимого (а иногда и достаточного) условия экстремума. Этот метод эффективен в случае малых выборок, но часто требует довольно сложных вычислений.
определяют на основе максимизации функции lnL. Для этого функцию исследуют на максимум с помощью необходимого (а иногда и достаточного) условия экстремума. Этот метод эффективен в случае малых выборок, но часто требует довольно сложных вычислений.
Пример. Найти методом наибольшего правдоподобия оценку параметра  в распределении Пуассона
в распределении Пуассона
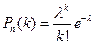
на основе проведенных опытов.
Решение. Будем называть опытом группу из n испытаний. При этом в каждом опыте фиксируется число появлений рассматриваемого события. Пусть таких опытов будет m. Тогда число появлений события в i-м опыте будет  . Подставляя полученное значение
. Подставляя полученное значение  в формулу Пуассона, получаем
в формулу Пуассона, получаем
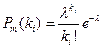
Эти вероятности 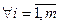 подставим в функцию правдоподобия
подставим в функцию правдоподобия
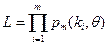 =
= 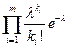
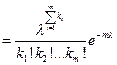
Находим логарифм этой функции
ln L= 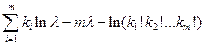
Возьмем первую производную по  и приравняем ее к нулю:
и приравняем ее к нулю:
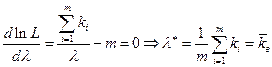

Если взять вторую производную, 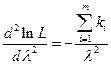 , то она отрицательна. Следовательно, полученное значение
, то она отрицательна. Следовательно, полученное значение  максимально.
максимально.
Литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2001
- Общий курс высшей математики для экономистов: Учебник. /Под ред.В.И.Ермакова.-М.:ИНФРА-М,20001.-656с

 . Допустим, что известен вид закона распределения вероятностей, но неизвестен параметр
. Допустим, что известен вид закона распределения вероятностей, но неизвестен параметр 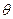 .
.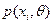 вероятность того, что величина X принимает значения
вероятность того, что величина X принимает значения 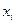 ,
, 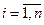 . Функцией правдоподобия дискретной случайной величины называют функцию
. Функцией правдоподобия дискретной случайной величины называют функцию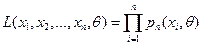 (54.1)
(54.1)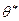 , при котором функция L принимает наибольшее значение. Эту оценку называют оценкой наибольшего правдоподобия.
, при котором функция L принимает наибольшее значение. Эту оценку называют оценкой наибольшего правдоподобия. в распределении Пуассона
в распределении Пуассона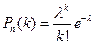
 . Подставляя полученное значение
. Подставляя полученное значение 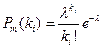
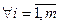 подставим в функцию правдоподобия
подставим в функцию правдоподобия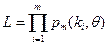 =
= 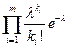
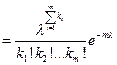
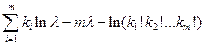
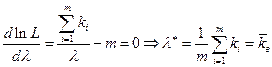

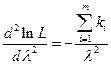 , то она отрицательна. Следовательно, полученное значение
, то она отрицательна. Следовательно, полученное значение  максимально.
максимально.


