Метод замены переменной в определенных интегралах
Теорема. Если функция f (x) непрерывна на отрезке [ a,b ], а функция x=j (t) дифференцируема на отрезке [ t 1, t 2], где a=j (t1) и b=j (t2), то имеет место формула:
Пример 2. Вычислить интегралы а) Решение. а) Сделаем замену
б) Сделаем тригонометрическую подстановку x = 4 sin t. Тогда
Заметим, что при использовании метода замены переменной необходимо проверять выполнение всех перечисленных в теореме условий. Если эти условия нарушаются, то может быть получен неверный результат.
9.5. Метод интегрирования по частям Теорема. Если функции u=u (x) и v=v (x) непрерывны вместе со своими производными на отрезке [ a,b ], то имеет место формула:
Пример 3. Вычислить интегралы а) Решение. а) Воспользуемся формулой (9.6) интегрирования по частям, для этого положим u=x, dv = e – xdx, откуда du=dx, v =– e–x. Тогда
б) Применяя формулу интегрирования по частям, получим
|

 . (9.5)
. (9.5)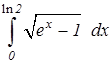 , б)
, б) 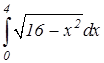 .
.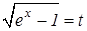 . Тогда
. Тогда 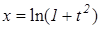 и
и 
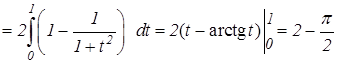 .
.
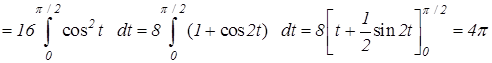 .
.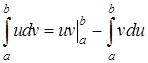 . (9.6)
. (9.6) , б)
, б)  .
.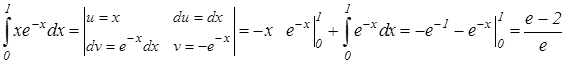 .
.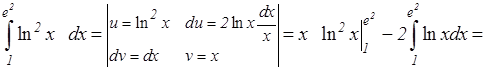
 .
.


