Понятие определенного интеграла
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ Понятие определенного интеграла Пусть функция f (x) определена на отрезке [ a,b ]. Этот отрезок разделим на n произвольных, необязательно равных, частей: a=x 0 < x 1 <... < xn=b. В этом случае говорят, что произведено разбиение отрезка [ a,b ]. На каждом участке разбиения [ xi –1, xi ] возьмем произвольную точку xi и вычислим значение функции f (x) в этих точках. Если умножить полученные значения функции f (xi) на длину соответствующего участка D xi = xi – xi –1 и просуммировать, то получим
которая называется интегральной суммой функции f (x) наотрезке [ a,b ]. Обозначим через D x =max D xi.
|
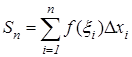, (9.1)
