Полярная система координат
Пусть кривая задана в полярных координатах уравнением: r=r(j), a£j£b, причем функция r(j) непрерывна и неотрицательна на отрезке [ a,b ]. Плоскую фигуру, ограниченную кривой r(j) и двумя лучами, составляющими с полярной осью углы a и b, будем называть криволинейным сектором (рис.9.12).
Площадь криволинейного сектора вычисляется по формуле:
Пример 11. Вычислить площадь ограниченной: а) лемнискатой Бернулли r 2= a 2cos 2j; б) трехлепестковой розой r = a cos 3j. Решение. а) Поскольку r 2³ 0, то cos 2j ³ 0. Отсюда получаем
где k ÎZ. Таким образом, данная кривая расположена в двух секторах (см. рис. 9.13). Для нахождения искомой площади достаточно вычислить четверть площади, а затем умножить ее на 4. Воспользуемся формулой 9.10:
б) Поскольку r ³ 0, то cos 3j ³ 0. Тогда получаем:
где k ÎZ. Таким образом, данная кривая будет расположена в трех секторах (см. рис. 9.14). Для нахождения искомой площади достаточно вычислить площадь половины одного "лепестка" и умножить ее на 6:
|


 . (9.10)
. (9.10)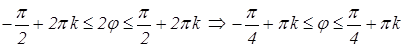 ,
,

 .
.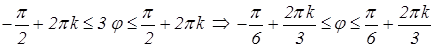 ,
,
 .
.


