Вычисление площади поверхности вращенияПусть функция f (x) неотрицательна и непрерывна вместе со своей производной на отрезке [ a,b ].Тогда площадь поверхности, образованная вращением графика этой функции вокруг оси Ox, будет вычисляться по формуле:
Пример 14. Вычислить площадь поверхности, образованной вращением вокруг оси Ox: а) отрезка прямой
б) Согласно формуле (9.14), получим
Замечание. При вычислении интеграла в) В параметрической форме формулу (9.14) можно записать в следующем виде:
Тогда площадь поверхности, образованной вращением одной арки циклоиды вокруг оси Ox, будет равна
г) Поскольку
д) Пусть дуга окружности с центром в начале координат и радиусом R вращается вокруг оси Ox. Из уравнения окружности x2+y2=R2 имеем y2=R2–x2, y¢y= –x, значит
Таким образом, площадь сферы S=4pR2.
|
. (9.14)
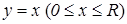; б) одной арки синусоиды y =sin x; в) одной арки циклоиды x=a (t –sin t), y=a(1 –cos t); г) параболы y 2= 2px, 0 £ x £ a; д) дуги окружности x2+y2=R2.
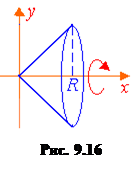Решение. а) Вычислим площадь поверхности, полученной вращением отрезка прямой 
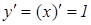. Подставляя в формулу (9.14) получим:
.
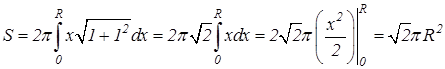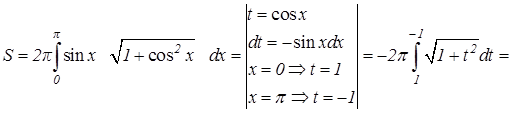
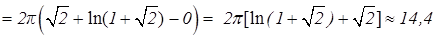(ед.кв.).
было использовано свойство 4 определенного интеграла (см. 9.2) и табличный интеграл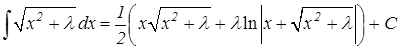 
(отметим, что этот интеграл можно было найти и методом интегрирования по частям).
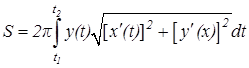. (9.15)
.
, 
, 
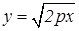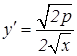, то по формуле (9.14) получим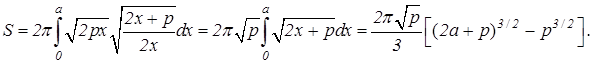
.
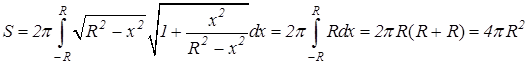