Параметрические функцииПусть верхняя граница криволинейной трапеции задана параметрическими уравнениями: x=x (t), y=y (t), t 1£ t £ t 2, причем x (t 1)= a, x (t 2)= b. Поскольку площадь криволинейной трапеции задается формулой S =
Пример 8. Вычислить площадь фигуры, ограниченной эллипсом (рис. 9.9):
Решение. Вычислим площадь верхней половины эллипса, а затем результат удвоим. Здесь x меняется от – a до a, следовательно, t должно изменяться от p до 0. Таким образом,
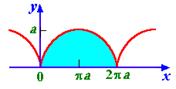
Пример 9. Вычислить площадь фигуры, ограниченной осью Oy и одной аркой циклоиды (см. рис. 9.10):
Решение. Для получения одной арки циклоиды, достаточно чтобы t изменялось от 0 до 2p. Тогда по формуле (9.9) получим
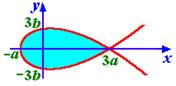
Пример 10. Вычислить площадь петли кривой (см. рис. 9.11):
Решение. Кривая пересекается с осью Ox в двух точках: x 1= – a и x 2= 3a при t 1= 0 и t 2,3=± 2. Площадь петли находим как удвоенную площадь верхней ее половины:
|
(если y (x)³ 0 на отрезке [ a,b ]), то, производя замену переменной, получим формулу для вычисления площади криволинейной трапеции, ограниченной кривой, заданной параметрически:
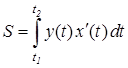(9.9)
.
.
.
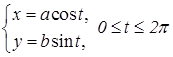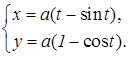
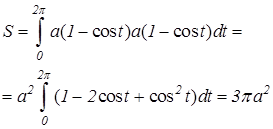
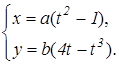
