Объем тела вращения
Если площадь
Выражение для функции
Если криволинейный сектор, ограниченный кривой
Отметим, что объемы тел значительно проще вычисляются при помощи кратных интегралов. Пример 15. Найти объем тела, образованного вращением фигуры, ограниченной а) линиями Решение. а) Используя формулу (9.17), найдем объем данного тела (рис. 9.17):
9.12. Физические приложения.
Работа, совершаемая переменной силой F (x) при перемещении материальной точки вдоль оси Ox, равна
Рассмотрим пример нахождения работы, которую необходимо затратить, чтобы выкачать жидкость плотности g из резервуара, имеющего вид тела вращения, получающегося при вращении криволинейной трапеции вокруг оси Oy. Пусть криволинейная трапеция в плоскости переменных ограничена линиями x = f (y)> 0, y = 0, y=H, x = 0. Элемент объема тела вращения равен элемент веса равен Умножая элемент веса на (H – yi) – высоту, на которую нужно поднять соответствующий вес при выкачивании жидкости – получим элемент работы:
Тогда работа по выкачиванию жидкости равна определенному интегралу по отрезку [ 0;H ]:
Пример 16. Вычислить работу, которую необходимо затратить, чтобы выкачать жидкость плотности g из резервуара, имеющего форму: а) конуса вращения с вершиной, обращенной вниз и совпадающей с началом координат, высота которого H, а радиус основания R; б) полусферы, обращенной выпуклостью вниз, радиус основания которой равен R; в) цилиндра высоты H и радиуса основания R.
б) Данная полусфера получается в результате вращения нижней четверти окружности
в) Данный цилиндр получается в результате вращения отрезка прямой
9. 13. Вычисление координат центра тяжести,
Пусть дуга кривой задана уравнением
Моменты инерции дуги этой кривой относительно координатных осей Ox и Oy равны:
Координаты центра тяжести дуги этой кривой вычисляются по формулам:
где l – масса дуги, определяемая по формуле:
Пример 17. Найти координаты центра тяжести дуги окружности
Тогда
9. 14. Вычисление координат центра тяжести,
Пусть плоская фигура ограничена кривой
Моменты инерции этой фигуры относительно координатных осей Ox и Oy равны:
Координаты центра тяжести плоской фигуры вычисляются по формулам:
где m – масса фигуры, определяемая по формуле:
Решение. Площадь полукруга равна
Так как фигура симметрична относительно оси Oy, то
По формуле 9.33, получаем:
Центр тяжести имеет координаты
|

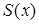 сечения тела плоскостью, перпендикулярной оси Ox, является непрерывной функцией на отрезке
сечения тела плоскостью, перпендикулярной оси Ox, является непрерывной функцией на отрезке 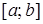 , то объем тела вычисляется по формуле:
, то объем тела вычисляется по формуле: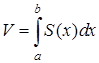 . (9.16)
. (9.16) , вращается вокруг оси Ox или оси Oy, то объемы тел вращения вычисляются по формулам:
, вращается вокруг оси Ox или оси Oy, то объемы тел вращения вычисляются по формулам: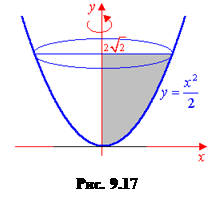
 или
или 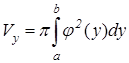 . (9.17)
. (9.17)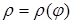 и лучами
и лучами  ,
,  , вращается вокруг полярной оси, то объем тела вращения равен:
, вращается вокруг полярной оси, то объем тела вращения равен: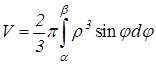 . (9.18)
. (9.18)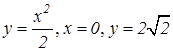 вокруг оси Oy; б) кардиоидой
вокруг оси Oy; б) кардиоидой 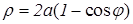 вокруг полярной оси.
вокруг полярной оси.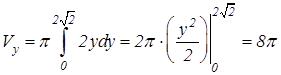 (ед. 3)
(ед. 3) б) Используя формулу (9.18), найдем объем данного тела (рис. 9.18):
б) Используя формулу (9.18), найдем объем данного тела (рис. 9.18):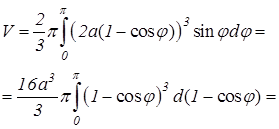
 .
. . (9.19)
. (9.19) ,
,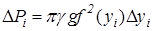 .
. .
. . (9.20)
. (9.20)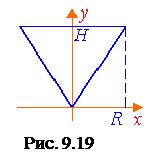 Решение. а) Данный конус получается в результате вращения прямой
Решение. а) Данный конус получается в результате вращения прямой  вокруг оси Oy (см. рис. 9.19). По формуле (9.20) находим
вокруг оси Oy (см. рис. 9.19). По формуле (9.20) находим .
. вокруг оси Oy (см. рис. 9.20). По формуле (9.20) находим
вокруг оси Oy (см. рис. 9.20). По формуле (9.20) находим
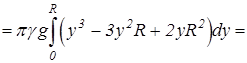
 .
. , 0 £ y £ H вокруг оси Oy. Тогда
, 0 £ y £ H вокруг оси Oy. Тогда .
. . Тогда статические моменты этой дуги относительно координатных осей Ox и Oy равны:
. Тогда статические моменты этой дуги относительно координатных осей Ox и Oy равны: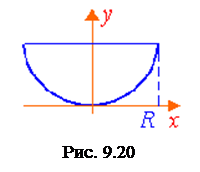
 , (9.21)
, (9.21)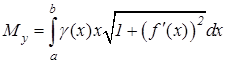 . (9.22)
. (9.22) , (9.23)
, (9.23)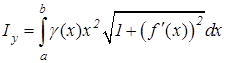 . (9.24)
. (9.24)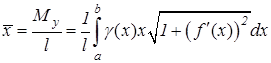 , (9.25)
, (9.25)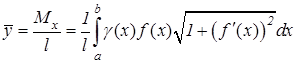 , (9.26)
, (9.26)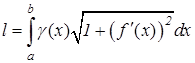 . (9.27)
. (9.27) (рис. 9.21), при условии
(рис. 9.21), при условии  .
. Решение. Длина дуги равна
Решение. Длина дуги равна 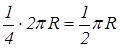 . Найдем массу этой дуги:
. Найдем массу этой дуги: 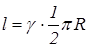 . Используя формулу 9.21, найдем статический момент:
. Используя формулу 9.21, найдем статический момент: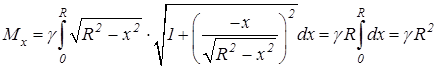 .
. . Учитывая симметричность дуги относительно биссектрисы координатного угла, получим
. Учитывая симметричность дуги относительно биссектрисы координатного угла, получим 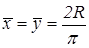 . Центр тяжести имеет координаты
. Центр тяжести имеет координаты  .
. и прямыми
и прямыми  , и имеет плотность
, и имеет плотность  , (9.28)
, (9.28) . (9.29)
. (9.29) , (9.30)
, (9.30) . (9.31)
. (9.31) , (9.32)
, (9.32)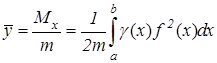 , (9.33)
, (9.33)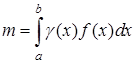 . (9.34)
. (9.34) Пример 18. Найти координаты центра тяжести полукруга
Пример 18. Найти координаты центра тяжести полукруга 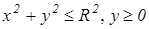 (рис. 9.22), при условии
(рис. 9.22), при условии  . Найдем массу этой фигуры:
. Найдем массу этой фигуры: .
.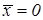 . Используя формулу 9.28, найдем
. Используя формулу 9.28, найдем 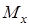 :
:
 .
.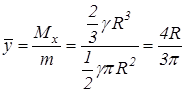 .
.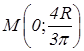 .
.


