Если предел последовательности интегральных сумм
существует, т.е. конечен и не зависит от способа разбиения отрезка [ a,b ] и от выбора точек xi на соответствующих участках, то этот предел называется Определенным интегралом функции f(x) на отрезке [ a,b ] и обозначают
Здесь число a называется нижним пределом, число b называется верхним пределом интеграла. Функция f (x) называется интегрируемой на отрезке [ a,b ], если для этой функции на указанном отрезке существует предел интегральных сумм, т.е. определенный интеграл. Необходимое условие интегрируемости: если функция f(x) интегрируема на отрезке [ a,b ], то она ограничена на этом отрезке. Достаточное условие интегрируемости: если функция f (x) непрерывна на отрезке [ a,b ], то она интегрируема на этом отрезке.
|
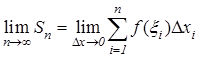. (9.2)
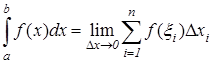. (9.3)
