Методами дифференциального исчисления.
Очевидно, функция определена на всей оси х.
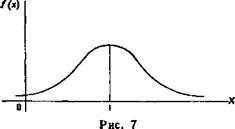
При всех значениях х функция принимает положительные значения, т. е. нормальная кривая расположена над осью Ох. Предел функции при неограниченном возрастании х (по абсолютной величине) равен нулю: lim у = 0, т. е. X 1 —со ось Ох служит горизонтальной асимптотой графика. Исследуем функцию на экстремум. Найдем первую производную: и' — fr~g_ е-(дс-а)г/(2а') а3 У^2п Легко видеть, что у'—О при х = а, уг>0 при х < а, у' < 0 при х > а. Следовательно, при л с —а функция имеет максимум, равный 1/(ст У2 я). Разность х —а содержится в аналитическом выражении функции в квадрате, т. е. график функции симметричен относительно прямой х = а. Исследуем функцию на точки перегиба. Найдем вторую производную: и"! e-(*-a)V(2<J») Г 1 У о3 У2п L в» У Легко видеть, что при х=а-\-а и х=а —о вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции равно 1/(о V 2л е)). Таким образом, точки графика ( а — а, 1/(аК2яе)) и (а + о, 1/(о ]/2яе)) являются точками перегиба. На рис. 7 изображена нормальная кривая при а = 1 и а = 2.
|