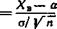Заменив неравенство в круглых скобках равносильным ему двойным неравенством, получим
P(X—tySlVK <a<X + tvSlVn) = y. Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал (х— tysjV~n, x+tyslVlT), покрывающий неизвестный параметр а с надежностью у. Здесь случайные величины X и S заменены неслучайными величинами х и s, найденными по выборке. По таблице приложения 3 по заданным пну можно найти tv. Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема п = 16 найдены выборочная средняя * = 20,2 и «исправленное» среднее квадратическое отклонение s = 0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95. Решение. Найдем ty. Пользуясь таблицей приложения 3, по ■у =0,95 н л=16 находим ty =2,13. Одиако важно подчеркнуть, что для малых выборок (п < 30), в особенности для малых значений п, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т. е. к повышению точности оценки. Например, если п = 5 и y«=0,99, то, пользуясь распределением Стьюдента, найдем ty = 4,6, а используя функцию Лапласа, найдем /т = 2,58, т. е. доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента. То обстоятельство, что распределение Стьюдента при малой выборке дает не вполне определенные результаты (широкий доверительный интервал), вовсе не свидетельствует о слабости метода Стьюдента, а объясняется тем, что малая выборка, разумеется, содержит малую информацию об интересующем нас признаке. Пояснение. Ранее было указано (см. гл. XII, § 14), что если Z —нормальная величина, причем M(Z)~ 0, a(Z)— 1, а V —независимая от Z величина, распределенная по закону х8 с k степенями свободы, то величина распределена по закону Стьюдента с к степенями свободы. Пусть количественный признак X генеральной совокупности распределен нормально, причем М(Х) = а, а(Х) = а. Если из этой совокупности извлекать выборки объема п и по ним находить выборочные средние, то можно доказать, что выборочная средняя распределена нормально, причем (см. гл. VIII, § 9) М(Хв) = а, о(Хл)=<з1Уп.
также имеет нормальное распределение как линейная функция нормального аргумента Хв (см. гл. XII, § 10, замечание), причем М (Z) — 0, a (Z) = 1. Доказано, что случайные величины Z и = ((п — 1) S2)/aa (***) независимы (S* — исправленная выборочная дисперсия) и что величина V распределена по закону с k — n —1 степенями свободы. Следовательно, подставив (**) и (***) в (*), получим величину Т = ((хв — а) V~ii)IS, которая распределена по закону Стьюдента с k — n —1 степенями свободы.
|