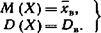Получим
М(Х) = хв. Математическое ожидание М (X), как видно из соотношения М (Х) = J xf (х; 0) Ле = ф (0), есть функция от 0, поэтому (*) можно рассматривать как уравнение с одним неизвестным 0. Решив это уравнение относительно параметра 0, тем самым найдем его точечную оценку 0*. которая является функцией от выборочной средней, следовательно, и от вариант выборки:
0* = Ф(*х. * Пример 1. Найти методом моментов по выборке xlt ха, х„ точечную оценку неизвестного параметра к показательного распределения, плотность распределения которого f(x) = \e-ljc (х^яО). Решение. Приравняем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: v1 = Af1. Учитывая, что v1 = Af(X), Mi=xB, получим М(Х)=хв. Приняв во внимание, что математическое ожидание показательного распределения равно 1/Л (см. гл. XIII, § 3), инеем k=l/xa. Итак, искомая точечная оценка параметра К показательного распределения равна величине, обратной выборочной средней: Б. Оценка двух параметров. Пусть задан вид плотности распределения f (х\ 01( 0Я), определяемой неизвестными параметрами 0А и 0Я. Для отыскания двух параметров необходимы два уравнения относительно этих параметров. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка: V1 = Mi, |Аа = /Ля. Учитывая, что vt = М (X), ця = D (X) (см. гл. VIII, § 10), Ml = xa, m2 = DB (см. гл. XVII, § 2), получим
Математическое ожидание и дисперсия есть функции от 0j н 0Я, поэтому (**) можно рассматривать как систему двух уравнений с двумя неизвестными и 0Я. Решив эту систему относительно неизвестных параметров, тем самым получим их точечные оценки 0J и 0J. Эти оценки являются функциями от вариант выборки: =^(*1, хя х„), = "Ф* (■*!» • • • * Хп)ш Пример 2. Найти методом моментов по выборке хи ха,..хп точечные оценки неизвестных параметров о и а нормального распределения Решение. Приравняем начальные теоретические и эмпирические моменты первого порядка, а также центральные и эмпирические моменты второго порядка: vi = Af1, 14=m,. Учитывая, что Vi = Af(X), (1*=1)(Х), Мх=хл, получим М(Х)=хш, D(X)=DM. Приняв во внимание, что математическое ожидание нормального распределения равно параметру а, дисперсия равна аа (см. гл. XII, § 2), имеем: а = хв, о 2 = £>„. Итак, искомые точечные оценки параметров нормального распределения: а*=1в> о* = VDB.
|