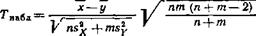Поскольку предположение о равенстве генеральных дисперсий выполняется, сравним средине.
Вычислим наблюдаемое значение критерия Стьюдента:
Подставив числовые значения величин, входящих в эту формулу, получим Тнабл —3,27. По условию, конкурирующая гипотеза имеет вид М (X) Ф М (К), поэтому критическая область—двусторонняя. По уровню значимости 05 и числу степеней свободы & = 5 + 6 — 2 = 9 находим по таблице (см. приложение 6) критическую точку *ЯВуст. кр (0.05; Э) = 2,26. Так как Т'набл > *двуст. кр — нулевую гипотезу о равенстве генеральных средних отвергаем. Другими словами, выборочные средние различаются значимо. Второй случай. Нулевая гипотеза Н0'.М(Х) = М (У). Конкурирующая гипотеза Ht:M (X) > М (У). В этом случае строят правостороннюю критическую область, исходя из требования, чтобы вероятность попада- „ лия критерия Т в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости: Если Тнабл > ^правост. кр —нулевую гипотезу отвергают. Третий случай. Нулевая гипотеза Н0:М(Х)~ = М (К). Конкурирующая гипотеза Ht:M (X) < М (К). В этом случае строят левостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости: Р {Т ^левост. up) = а* В силу симметрии распределения Стьюдента относительно НУЛЯ fлевост. кр = ~ *правост. кр- Поэтому Сначала НЭ- ходят «вспомогательную» критическую точку /праВост. кр так, как описано во втором случае, и полагают ^левост. кр =я ^правост. кр* Если Тнабл > — Завоет, кр—отвергнуть нулевую гипотезу нет оснований. Если Г„абл < — *npaB0CT. кр—нулевую гипотезу отвергают.
|