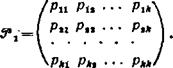Таким образом, случайное блуждание — пример однородной цепи Маркова с дискретным временем.
Далее ограничимся элементами теории конечных однородных цепей Маркова. Переходной вероятностью р1} называют условную вероятность того, что из состояния i (в котором система оказалась в результате некоторого испытания, безразлично какого номера) в итоге следующего испытания система перейдет в состояние /. Таким образом, в обозначении р{) первый индекс указывает номер предшествующего, а второй—номер последующего состояния. Например, рп — вероятность «перехода» из первого состояния в первое; ргз — вероятность перехода из второго состояния в третье. Пусть число состояний конечно и равно к. Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:
Так как в каждой строке матрицы помещены вероятности событий (перехода из одного и того же состояния в любое возможное состояние /), которые образуют полную группу, то сумма вероятностей этих событий равна единице. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице: Pt/=l (*=1,2 к). Приведем пример матрицы перехода системы, которая может находиться в трех состояниях: /0,5 0,2 0,3\ 0,4 0,5 0,1. \0,6 0,3 0,1/ Здесь р11 = 0,5 — вероятность перехода из состояния = 1 в это же состояние /==1; ргх — 0,4 — вероятность перехода из состояния i — 2 в состояние } — 1. Аналогичный смысл имеют остальные элементы матрицы.
|