Декартова система координат
Нехай у просторі задана точка О і три некомпланарних вектори е1, е2, е3. Декартовою системою координат у просторі (на площині) називається сукупність точки й базису, тобто сукупність точки й трьох некомпланарних векторів (2-х неколінеарних векторів), що виходять із цієї точки. Точка О називається початком координат; прямі, що проходять через початок координат у напрямку базисних векторів, називаються осями координат - віссю абсцис, ординат і аплікат. Площини, що проходять через осі коор-
Розглянемо в обраній системі координат довільну точку М. Уведемо поняття координати точки М. Вектор ОМ, що з'єднує початок координат із точкою М називаєтьсяі радіусом-вектором точки М. Векторові ОМ в обраному базисі можна зіставити трійку чисел - його координати: ОМ = хе1 + уе2 + 2е3. Координати радіуса-вектора точки М називаються координатами точки М у розглянутій системі координат М(х,у,г). Перша координата називається абсцисою, друга - ординатою, третя - аплікатою.
Аналогічно визначаються декартові координати на площині. Тут точка має тільки дві координати - абсцису й ординату.
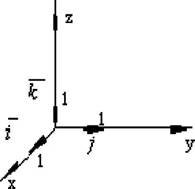
Рис. 3.19. Декартова прямокутна система координат При заданій системі координат кожна точка має визначені координати. З іншого боку, для кожної трійки чисел знайдеться єдина точка, що має ці числа як координати. Якщо вектори, узяті як базис, в обраній системі координат, мають одиничну довжину й попарно перпендикулярні, то система координат називається декартовою прямокутною системою координат. Основні вектори прийнято позначати буквами і,у,к, а осі координат Ох, Оу і Оі, а будь-який вектор у цій
системі координат можна записати у вигляді: а = хі + у] + ік.
|

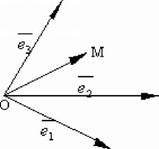 Рис. 3.18. Точка М у базисі векторів е1, е2, е3
Рис. 3.18. Точка М у базисі векторів е1, е2, е3