Базис, розкладання вектора за базисом. Ортогональні системи векторів. Перехід від одного базису до іншого
Базисом називається сукупність відмінних від нуля лінійно незалежних векторів. Елементи базису будемо позначати е1,е2,...,ек. У попередньому параграфі ми довели, що два неколінеарних вектори на площині лінійно незалежні, відповідно до теореми 1 (будь-які два вектори лінійно залежні тоді й тільки тоді, коли вони колінеарні). Отже, базисом на площині є будь-які два неколінеарних вектори на цій площині. Аналогічно у просторі лінійно незалежні будь-які три некомпланарних вектори. Отже, базисом у просторі назвемо три некомпланарних вектори. Справедливе наступне твердження. Теорема 3. Нехай у просторі заданий базис е1, е2, е3. Тоді будь-який вектор а можна представити у вигляді лінійної комбінації а = хе1 + уе2 + ze3, де х, у, z - деякі числа. Таке розкладання єдине.
Рис. 3.16. Розкладання вектора а за векторами е1,е2,е3 у просторі Як частину випадку із цієї ж теореми можна сформувати наслідок: Якщо задано базис е1, е2 на площині, то будь-який вектор, компланарний з векторами е1, е2 можна перетворити у вигляд а = хе1 + уе2, причому таке розкладання єдине.
Таким чином, базис дозволяє знайти однозначне співвідношення кожного вектора до трійки чисел - коефіцієнтів розкладання цього вектора за векторами базису: а ^ (х, у, z). Вірно й зворотне, з кожної трійки чисел х, у, z за допомогою базису можна утворити вектор, якщо скласти лінійну комбінацію хе1 + уе2 + ze3 = а. Якщо е1, е2, е3 базис і а = хе1 + уе2 + ze3, то числа х, у, z називаються координатами вектора а у даному базисі. Координати вектора а позначають а = (х, у, z).
|


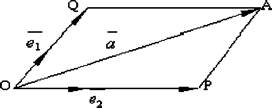 Рис. 3.17. Розкладання вектора а за векторами е1,е2 на площині
Рис. 3.17. Розкладання вектора а за векторами е1,е2 на площині



