Кут між векторами. Проекція вектора на вісь
Нехвй у просторі дані два вектори а і Ь. Відкладемо від довільної точки О вектори ОА = а і ОВ = Ь. а
Кутом між векторами а і Ь називається найменший з кутів АЛОБ. Кут між векторами позначається (а; Ь) = 0 <ф<ж. Розглянемо вісь І і відкладемо на ній одиничний вектор е (тобто вектор, довжина якого дорівнює одиниці).
0 е І Рис. 3.11. Кут між вектором а і віссю І Під кутом між вектором а і віссю І розуміють кут р між векторами а і е. Отже, нехай І - деяка вісь і а = АВ- вектор. Позначимо через А1 і В1 проекції на вісь І відповідно точок А і В. Припустимо, що А1 має координату х1, а В1 - координату х2 на осі І. Тоді проекцією вектора АВ на вісь І називається різниця х2 - х1 між координатами проекцій кінця і початку вектора АВ на цю вісь.
Проекцію вектора а на вісь І будемо позначати пріа = пріАВ. Ясно, що коли кут між вектором а і віссю І гострий, то х2> х1, і проекція х2 -.х1> 0; якщо цей кут тупий, то х2< х1 і проекція х2 - х1< 0. Нарешті, якщо вектор а перпендикулярний осі І, то х2= х1 і х2- х1= 0. Таким чином, проекція вектора АВ на вісь І - це довжина відрізка А1В1, узята з відповідним знаком. Отже, проекція вектора на вісь це число або скаляр. Аналогічно визначається проекція одного вектора на іншій. У цьому випадку знаходяться проекції кінців даного вектора на ту вісь, на якій лежить другий вектор. Розглянемо деякі осно вні властивості проекцій. 1. Проекція вектора а на вісь І дорівнює добуткові модуля вектора а на
косинус кута між вектором і віссю: пр1 а =
2. Проекція суми двох векторів на вісь дорівнює сумі проекцій векторів на ту ж вісь: пр1 (а + Ь) = пр{а + пргЬ. Наслідок. Проекція різниці двох векторів на вісь дорівнює різниці проекцій цих векторів на ту ж вісь.
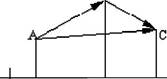
4 в, с, - Рис. 3.14. Проекція суми двох векторів Цю властивість можна узагальнити на випадок будь-якого числа додан ків. 3. Якщо ненульовий вектор а збільшується у X разів, то його проекція на вісь також збільшується на це число: прі (Ла) = Л ■ пріа.
|

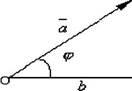

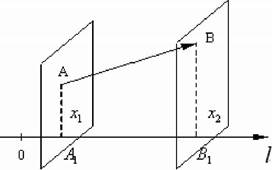 Рис. 3.12. Проекція вектора АВ на вісь І
Рис. 3.12. Проекція вектора АВ на вісь І
 0 _ 1
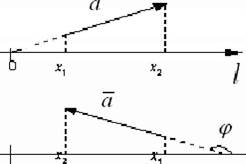
Рис. 3.13. Проекція вектора а на вісь І, через кут між вектором і віссю
0 _ 1
Рис. 3.13. Проекція вектора а на вісь І, через кут між вектором і віссю