Лінійні операції над векторами
Множення вектора на число Добутком вектора а на число X називається новий вектор Ь такий, що: 1.Ь = ЩЦ; 2. Вектор Ь о кооінеарним векторові а; 3. Вектори Ь і а спрямовані однаково, яощо X > 0 і протилежно, якщо X < 0. (Якщо X = 0, то з умови 1 випливає, що Ь = 0). Добуток вектора а на число X позначається Л • а. Наприклад, 1 а цє вектор, спрямований у той же бік, що і вектор а, і має довжину, удвічі меншу, ніж вектор а. Операція множення має такі властивості: 1. Для будь-яких чисел а і в і вектора а виконується рівність а(р а о) = (ар)а. Дійсно, вектори, що знаходяться в обох частинах рівності, мають однакову довжину І а| - |в| • |а|. Крім того, ясно, що вони однаково спрямовані, тому що їхній напрямок збігається з напрямком вектора а, якщо а і | одного знака, і протилежно спрямовані а, якщо а і | різних знаків. 2. Нехай даний вектор а Ф 0. Для будь-якого колінеарного йому вектора Ь існує і до того ж тільки одне число X, що задовольняє рівності Ь = Л • а. Число X має тільки одне значення тому, що при множенні вектора а на два різних числа, одержуємо два різних вектори. Додавання некторів Нехай а в Ь - два довільних вектори. Візьмемо довільну тонку О і побу- дунмо вектор ОА = а. Після цього з точки А відкладемо вектор АВ = Ь. Вектор ОВ, що з'єднує початок першого некноро а с кінцем другого Ь, називається сумою цих векторів і позначається а + Ь = ОА + АВ.
Сформульоване визначення додавання векторів називають правилом паралелограма, тому що ту ж саму суму векторів можна одержати у такий спосіб: відкладемо від точки О вектори ОА = а і ОС = Ь; побудуємо на цих векторах паралелограм ОАВС. Оскільки вектори ОС = АВ, то вектор ОВ, щн є ніагонал- лю паралелограма, проведеної з вершини О, буде сумою векторів а + Ь.
Легко перевірити наступні властивості додавання векторів. 1. Ясно, що додавання нульового вектора до будь-якого вектора а не змінює вектора а, тобто а + 0 = а. 2. Додавання векторів є комутативним, тобто а + Ь = Ь + а. Ця властивість відразу випливає із правила паралелограма. 3. Додавання векторів асоціативно, тобто для будь-яких трьох векторів а + (Ь + с) = (а + Ь) + с. Тому суму трьох векторів часто записують просто а + Ь + с. Суму трьох векторів можна одержати у такий спосіб. З довільної точки О відкладається вектор, що дорівнює першому векторові. До його кінця приєднується початок другого, до кінця другого - початок третього. Вектор, що з'єд Ь
4. Для будь-якого числа X і будь-яких векторів а і Ь:
Зауважимо, що при множенні векторів на число X змінюються тільки розміри векторів, тобто масштаб креслення; фігури залишаються подібними. Оскільки вектори а, Ь і а + Ь утворять сторони і діагональ паралелограма, то, помноживши всі члени на X, тобто змінивши лише розміри векторів однаковим чином, ми одержимо знову паралелограм, а виходить, збережеться рівність Я- а + Я-Ь = Я-(а + Ь). 5. Для будь-яких чисел а і Ь і будь-якого вектора а виконується рівність (а + в)а = а- а + а. Різниця векторів
Вектор, колінеарний даному векторові а, рівний йому за довжиною і протилежно спрямований, називається протилежним вектором для вектора а і позначається -а або а. в Протилежний вектор а можна розглядати як результат множення вектора а на число X = -1: —а = (-1)- а.
Різницею двох векторів а і Ь називається вектор с = а — Ь, що дорівнює сумі векторів а і — Ь, тобто с = а +. Зрозуміло, що а — а = а + (—а) = 0 для будь-якого вектора а. Легко довести, що Ь + (а — Ь) = а. Таким чином, якщо с = а — Ь, то Ь + с = а. З визначення суми двох векторів випливає правило побудови вектора- різниці. Відкладаємо вектори ОА = а і ОВ = Ь із спільної точки О.
Щоб знайти веквор-ріпницю, потрібно до ОА додати вектор —ОВ або ВО. Тоді ОА + ВО = ВО + ОА = ВА. Вектор ВА, що з'єднує кінці векторів а, Ь і спрямований від «від'ємника» по «зменшуваного» (тобто від другого вектврп до першого), і Пудп ріпницею а — Ь. Дійсно, за правилом додавання векторів ВО + ВА = ОА або Ь + с = а. Таким чином, якщо на векторах а і Ь, відкладених із спільної точки О, побудувати паралелограм ОАСВ, то вектоп ОС, що збігається з більшою діагоналлю паралелограма, дорівнює сумі а + Ь, а вектор ВА, що збігається з меньшою діагоналлю, дорівнює різниці а — Ь.
|

 Рис. 3.4. Сума двох векторів
Рис. 3.4. Сума двох векторів
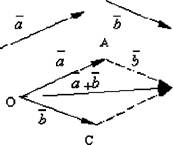 Рис. 3.5. Правило паралелограма
Рис. 3.5. Правило паралелограма
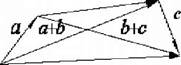 а+Ь+с
Рис. 3.6. Сума трьох векторів
а+Ь+с
Рис. 3.6. Сума трьох векторів

 Рис. 3.7. Четверта властивість додавання векторів
Рис. 3.7. Четверта властивість додавання векторів
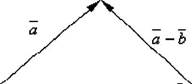 о І
Ь
Рис. 3.8. Різниця двох векторів
о І
Ь
Рис. 3.8. Різниця двох векторів

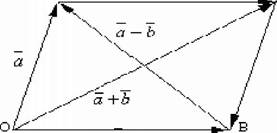 і
Рис. 3.9. Правило побудови вектора різниці
і
Рис. 3.9. Правило побудови вектора різниці



