Скалярний добуток векторів і його властивості
Вище ми розглянули множення вектора на число. Але у багатьох задачах зустрічається операція множення вектора на вектор. Але при цьому результат може бути як числом, так і вектором. Тому розглядають два види множення векторів: скалярне й векторне. Нехай дані два вектори а і Ь, кут між якими дорівнює (— (аЬ Скалярним добутком векторів а і Ь називається число, рівне добуткові довжин цих векторів на косинус кута між ними. Скалярний добуток познача
ється а • Ь. Отже, а • Ь
Якщо один із векторів нульовий, то скалярний добуток вважається рівним нулю. Розглянемо властивості скалярного добутку. 1. Скалярний добуток двох векторів підкоряється комутативному законові, тобто для будь-яких векторів а і Ь а • Ь = Ь • а. 2. Для будь-якого числа X і будь-яких векторів а і Ь маємо: Л(а • Ь) = (а)• Ь = а •(Ь). 3. Для будь-яких векторів а,Ь, с виконується рівність: (а + Ь)• с = а • с + Ь • с.
4. Для будь-якого вектора а виконується співвідношення а — а • а
—л/а — уЛ Із цієї властивості зокрема випливає
5. Скалярний добуток двох векторів дорівнює нулю тоді й тільки тоді, коли дорівнює нулю один зі співмножників або вектори перпендикулярні. Це властивість очевидна з визначення скалярного добутку. Таким чином, необхідною й достатньою умовою ортогональності двох ненульових векторів є рівність нулю їхнього скалярного добутку.
|
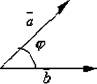Рис. 3.24. Скалярний добуток векторів
