Мішаний добуток векторів і його властивості
Мішаним добутком трьох векторів а, Ь, с називають число, отримане векторним множенням перших двох векторів, з наступним скалярним множенням отриманого вектора а х Ь на третій вектор с. Позначається мішаний добуток (аЬс) _ (ахЬ) • с. Зрозуміло, такий добуток є число. Розглянемо властивості мішаного добутку. 1. Геометричний зміст мішаного добутку. Мішаний добуток трьох векторів із точністю до знака дорівнює об'єму паралелепіпеда, побудованого на
цих векторах, як на ребрах, тобто (аЬс) _ ±Уп парал •
Таким чином, об'єм паралелепіпеда ї^тарап = і об'єм піраміди (тетраедра) КпИрам =1 (аЬс)
Якщо трійка векторів а, Ь, с права, то мішаний добуток (аЬс)> 0, а якщо а, Ь, с - ліва, то (аЬс) < 0. 2. Для будь-яких векторів а, Ь, с справедлива рівність: (аЬс) = (ах Ь) • с = а • (Ь х с) 3. При перестановці будь-яких двох співмножників мішаний добуток змінює знак. Дійсно, якщо розглянемо мішаний добуток (аЬс), то, наприклад, (Ьас) = (Ьха) • с = -(ахЬ) • с = -(аЬс). 4. Мішаний добуток (аЬс) = 0 тоді і тільки тоді, коли один зі співмножників дорівнює нулю або вектори а, Ь, с - компланарні. 5. Якщо вектори задані у координатній формі а = х1 і + у1 у + z1 к й Ь = х2 і + у2 у + z2 к і с = х3 і + у3 у + z3 к, то можна довести, що їхній мішаний добуток знаходиться за формулою:
х1 У1 х У2
У3
Таким чином, мішаний добуток (аЬс) дорівнює визначникові третього порядку, рядки якого складаються з координат першого, другого і третього векторів. Умова компланарності трьох ненульових векторів Із властивостей мішаного добутку, необхідною й достатньою умовою компланарності трьох векторів є рівність нулю їхнього мішаного добутку. Крім того, авідси випливає, що три вектори а, Ь, с утворюють базис у просторі, якщо (аЬс) Ф 0.
|

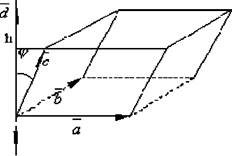 Рис. 3.29. Геометричний зміст мішаного добутку
Рис. 3.29. Геометричний зміст мішаного добутку



