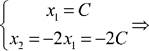Приклади. Приклад 1. Знайти власні вектори й відповідні їм власні значення мат­

Приклад 1. Знайти власні вектори й відповідні їм власні значення мат­. Знайти представлення матриці А у базисі, утвореному її влас-

ними векторами. А Складемо характеристичне рівняння

О.

V ^{8 3})

І -Я І 8 З -Я

риці Л

Розкриваючи визначник, одержуємо квадратне рівняння, з якого знайде-

 

мо власні значення:

 

[(і-Я)(3-Я)-8 = О]^[Я² -4Я-5 = О] Я =-1;Я =5.

Перший розв'язок Я₁ = -1.

Підставляємо у характеристичне рівняння значення Я₁ = -1 та одержимо систему рівнянь:

2 x₁ + x₂ = О Г 2 x₁ + x₂ = О Г 2 x₁ + x₂ = О, 8 x₁ + 4 x₂ = О ^ [2x₁ + x₂ = О ^ [ О = О.

Останнє рівняння системи обернулося на нуль, і система стала недовизначеною - два рівняння на три невідомих. Ранги основної матриці системи і розширеної матриці збігаються (рівні 1), але менше розмірності системи (кількості невідомих рівних 2), тобто:

rang Л = rang Л* < n.

Запишемо розв'язок системи у такий спосіб:

Г С 1

Хі =, де CeR.

v ^2С У

Г і 1

Тобто, при C=1 довільний частинний розв'язок Х₁ =.

V^-2 У

C

C

Другий розв'язок Я₂ = 5.

де СєЯ. 'О v 4 У

-4 x₁ + х₂ = 0

X,

^ X₂ =

4 C

8х₁ - 2х₂ = 0 [х₂ = 4x₁ = 4C Тобто, при С=1 довільний частинний розв'язок X₂

 

Зробимо перевірку за допомогою пакета Maxima. Для обчислення влас­них значень і власних векторів необхідно за допомогою оператора matrix вве­сти матрицю, що задана в умові завдання.

Щоб знайти власні значення матриці використовують функцію eigenvalues. Ця функція виводе список, що складається із двох підсписків. Перший підсписок - це власні значення матриці A, а другий підсписок - це сту­пінь складності власних значень у відповідному порядку.

Функція eigenvalues викликає функцію solve, щоб знайти розв'язки характеристичного рівняння матриці. Іноді функція solve не здатна знайти розв'язки багаточлена через те, що вони є комплексними числами.

Щоб знайти власні вектори матриці необхідно використовувати функ­цію eigenvectors. Ця функція створює список, у якому перші два підсписки - це власні значення матриці та ступінь складності власних значень, а інші під- списки - це власні вектори матриці, що відповідають цим власним значенням.

(%il) A: matrix ([1,1], [8,3])?

(%І2) eigenvalues(%);

(%о2) [[5,-1], [1,1]]

(%ІЗ) eigenvectors(А);

(%оЗ) [[[5,-1], [1,1]], [1, 4 ], [1,-2]] Рис. 3.31. Пошук власних значень і власних векторів матриці

Таким чином, за допомогою пакета Maxima одержимо власні значення

1 4

1 Ч—2У

рами: A =

ґл\ f 1 \

матриці А: \ = 5; Я₂ =—1, і власні вектори: X₁ Тепе

X

р представимо матрицю А у базисі, утвореному її власними векто- -1 0 0

Приклад 2. Знайти власні вектори й відповідні їм власні значення мат- ^Ґ1 -1 0^Л

риці A =

2 1

1 -1 -1 0

У

Складемо характеристичне рівняння:

1 -Л -1 0

2 1 -Л -1 = 0.

1 -1 0 -Л

Розкриваємо визначник розкладанням за першим рядком:

1 л _ 1 2 __ 1

(1 -Л) _{- 1 -Л}+ 1_{1 -Л}=(1 -Л)(Л-Л- 1)-2 Л + 1 =

= Л² -Л-1 -Л³ +Л² + Л-2Л +1 = Л(-Л² + 2Л-2) = 0.

Оскільки вираз у дужках не має раціональних розв'язків (дискримінант В = Ь² - 4ас = 2² - 4 • 2 = -4 < 0) маємо єдиний розв'язок Л = 0.

Підставляючи власне значення у характеристичне рівняння, одержуємо систему рівнянь:

с 3 Є-

0

Хі Х ґ%

Х 1 — Х 2 Хо — 3 х0

с

2 Х1 х 2

0

X

Хл

 

с є Я

3 с

V ' 1 ^ 1 3

У

х₁ - х₂ = 0

Тобто, при С=1 довільний частинний розв'язок X ■

 

3.24. Лінійна модель обміну (модель міжнародної торгівлі)

Як приклад математичної моделі економічного процесу, що зводиться до поняття власного вектора і власного значення матриці, розглянемо лінійну мо­дель обміну (модель міжнародної торгівлі).

п Е ау	= 1(7=1,	2,.,
/=1
г а11	а12 —	а1п ^
а21	а22 —	а2 п
V ап1	ап 2 —	апп У

Нехай маємо п країн £_ь Б₂,..., Б_п національний прибуток кожної з яких дорівнює відповідно х₁, х₂,..., х_п. Позначимо коефіцієнтами ау частину націо­нального прибутку, що країна Бу витрачає на покупку товарів у країни 5/. Буде­мо вважати, що увесь національний прибуток витрачається на закупівлю това­рів або всередині країни, або на імпорт з інших країн, тобто:

Розглянемо матрицю А = що одержала назву структурної матриці торгівлі. Відповідно до формули

п

Е ау = 1, сума елементів будь-якого стовпця матриці А дорівнює 1.

Для будь-якої країни Б (/=1, 2,..., п) виторг від внутрішньої й зовнішньої
торгівлі складе:

Рі = ^аі1^[11]1 + ^аі2^Х2 + ••• + ^аіп^Хп. Для збалансованої торгівлі необхідна бездефіцитність торгівлі кожної

країни Б_і, тобто виторг від торгівлі кожної країни повинний бути не менше її національного прибутку:

Рі > Х (і=1, 2,..., п). Якщо вважати, що р_і > х_і (і=1, 2,..., п), то одержуємо систему нерівнос­тей:

^а11^Х1 + ^а12^Х2 + • + ^а1п^Хп > ^Х1^{, а}21^Х1 + ^а22^Х2 + • + ^а2п^Хп > ^Х2,

^ап1^Х1 + ^ап2^Х2 + ••• + ^апп^Хп > ^Хп.

Склавши і згрупувавши всі нерівності останньої системи, одержимо:

^Х1 (^а11 + ^а21 + ••• + ^ап1) + ^Х2 (^а12 + ^а22 + ••• + ^ап2) + ••• • + ^Хп (^а1п + ^а2п + • + ^апп)> ^Х1 + ^Х2 + ••• + ^Хп.

п

З огляду на ^ а^ = 1, вирази в дужках рівні одиниці, і ми приходимо до

і=1

суперечливої нерівності: Х₁ + Х₂ + •.. + Х_п > Х₁ + Х₂ + •.. + Х_п.

Таким чином, нерівність р_і > Х_і (і=1, 2,_, п) неможлива, і умова р_і > Х_і приймає вид р_і = Х_і(і=1, 2,..., п). З економічної точки зору це зрозуміло, тому що всі країни не можуть одночасно діставати прибуток.

 

' Х1 Л Х

Уводячи вектор X

національних прибутків країн, одержимо рів-

Розв'язуючи останню систему методом Гаусса знаходимо: х₁ =(3/2) С,

 

— 2 С, Х3 — С.

Отриманий результат означає, що збалансованість торгівлі трьох країн досягається при векторі національних прибутків х — (3/2С;2С;С), тобто при співвідношенні національних прибутків країн 3: 4: 2. ►