Індивідуальне завдання № 3.5

Студент повинен розв'язати одну з наведених нижче задач, вибравши її за своїм номером у журналі групи.

З'ясувати компланарні чи некомпланарні вектори а, Ь і С?

1. а = {2, 3, 1}, Ь ={-1, 0, -1}, с = {2, 2, 2}.

2. а = {3, 2, 1}, Ь ={2, 3, 4}, с = {3, 1, -1}.

3. а = {1, 5, 2}, Ь ={-1, 1, -1}, с = {1, 1, 1}.

4. а = {1, -1, -3}, Ь ={3, 2, 1}, с = {2, 3, 4}.

5. а = {3, 3, 1}, Ь ={1, -2, 1}, с = {1, 1, 1}.

6. а = {3, 1, -1}, Ь ={-2, -1, 0}, с = {5, 2, -1}.

7. а = {4, 3, 1}, Ь ={1, -2, 1}, с = {2, 2, 2}.

8. а = {4, 3, 1}, Ь ={6, 7, 4}, с = {2, 0, -1}.

9. а = {3, 2, 1}, Ь ={1, -3, -7}, с = {1, 2, 3}.

= 15 Ф 0, тобто векто­

10. а = {3, 7, 2}, Ь ={-2, 0, -1}, с = {2, 2, 1}.

11. a =	1,	-2,	6}, Ь	= { 1, 0, 1}, c = { 2, -6, 17}.
12. a =	6,	3,	4}, Ь =	= {-1, -2, -1}, c = { 2, 1, 2}.
13. a =	7,	3,	4}, Ь =	= {-1, -2, -1}, c = { 4, 2, 4}.
14. a =	2,	3,	2}, Ь =	= { 4, 7, 5}, c = { 2, 0, -1}.
15. a =	5,	3,	4}, Ь =	= {-1, 0, -1}, c = { 4, 2, 4}.
16. a =	3,	10,	5}, Ь	= {-2, -2, -3}, c = {2, 4, 3}
17. a =	-2,	-	4, -3},	Ь ={4, 3, 1}, c = {6, 7, 4}.
18. a =	3,	1,	-1}, ь	= {1, 0, -1}, c = {8, 3, -2}.
19. a =	4,	2,	2}, Ь =	-{-3, -3, -3}, c = {2, 1, 2}.
20. a =	4,	1,	2}, Ь =	:{9, 2, 5}, c = {1, 1, -1}.
21. a =	5,	3,	4}, Ь =	= {4, 3, 3}, c = {9, 5, 8}.
22. a =	3,	4,	2}, Ь =	= {1, 1, 0}, c = {8, 11, 6}.
23. a =	4,	-1,	-6},	Ь ={1, -3, -7}, c = {2, -1, -
24. a =	3,	1,	0}, Ь =	{-5, -4, -5}, c = {4, 2, 4}.
25. a =	3,	0,	3}, ь =	= {8, 1, 6}, c = {1, 1, -1}.
26. a =	1,	-1,	4}, Ь	= {1, 0, 3}, c = {1, -3, 8}.
27. a =	6,	3,	4}, Ь =	= {-1, -2, -1}, c = {2, 1, 2}.
28. a =	4,	1,	1}, Ь =	{-9, -4, -9}, c = {6, 2, 6}.
29. a =	-3,	3,	3}, Ь	= {-4, 7, 6}, c = {3, 0, -1}.
30. a =	-7,	10, -5},	Ь ={0, -2, -1}, c = {-2, 4,
31. a =	7,	4,	6}, ь =	-{2, 1, 1}, c = {19, 11, 17}.

 

3.20. Висота тетраедра (піраміди)

У деяких задачах на застосування мішаного добутку векторів потрібно знайти висоту піраміди (тетраедра) при відомих координатах її вершин. Така задача зустрічається й в аналітичній геометрії, при обчисленні відстані від точ­ки до площини, що проходить через три точки.

Нехай дана піраміда з вершинами у точках Л₁, Л₂, Л₃, Л₄. Потрібно знай­ти висоту опущену з вершини Л₄ на грань ЛЛ₂Л₃.

З вершини Лі проведемо 3 вектори й знайдемо їхні координати:

^Лі^Л₂ = (^х2 ^{— х}і^; У₂ ^- Уі^{; 2}₂ ^- •)^{, Л}_і^Л₃ = (^{— х}₁^{; у}₃ ^{- у}₁^; • ^- •)^{, Л}₁^Л₄ = (^х₄ ^{— х}₁^{; у}₄ ^{- у}₁^{; —} •)

V

А1А2А3А4

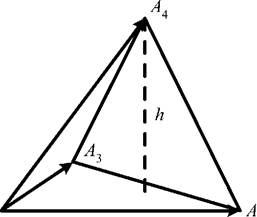Рис. 3.30. Піраміда з вершинами у точках А1, А2, А3, А4

А,

З курсу елементарної геометрії відома формула для об'єму тетраедра: 1 3Г_Л

^А1^А2^А3^А4

—_{А А} • к. Звідки к

3 ^А1^А2^А3 5

^А1^А2^А3

 

З іншого боку, об'єм тетраедра знайдемо відповідно до геометричного змісту мішаного добутку:

V

А1А2А3А4

(А1 ^ А1А3 А1А4) =

1

(^А1^А2 ^А1^А3 ^А1Л)

Мішаний добуток векторів (А1А2 А1А3 А1А4 дорівнює визначникові тре­тього порядку, рядки якого складаються з координат першого, другого і третьо­го векторів.

^Х2 ^Х1 У 2 ^у1 ²2 ²1

^Х3 ^-Х1 ^у3 ^{- у}1 ^г3 ^-

^Х4 ^Х1 ^у4 ^у1 ^г4

Площу основи тетраедра (трикутника) знайдемо використовуючи векто­рний добуток векторів 5_АіАгАз = 1 (А₁А₂ х А₁А₃).

Координати векторного добутку (А₁А₂ х А₁А₃) знайдемо як:

(А1А2 х А1А3)

г ] к

^Х2 ^Х1 ^у2 ^у1 ^Х3 ^{- Х}1 ^у3 ^{- у}1 ^г3 ^-

Остаточно, висота тетраедра:

 

3 • І 6

3V к = А1А2А3А4 А1А2А3

(^А1^А2 ^А1^А3 ^А1^А4)| (Аг А1А3 АА)

¹ (А₁А₂ х А₁А₃) (^А1^А2^{х А}1^А3) ' 139