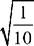Квадратичну форму звести до канонічного вигляду ортогональним пере-
\ 2 2 х1,х2) = 2х1 - 6х1 х2 +10х2.
Л Знайдемо матрицю первинної квадратичної форми. її діагональні елементи дорівнюють коефіцієнтам при квадратах змінних, тобто 2, 10, а інші елементи - половинам відповідних коефіцієнтів квадратичної форми, тобто ' 2 -3Л
А
ч-3 10У
Складаємо характеристичне рівняння для матриці А:
і „ і 2-Я -З А-ЯЕ = = 0
1 1 -3 10 -Я
Розкриваємо визначник (2-Я)(10-Я)-(-3)(-3) = 0,
20-2Я-10Я + Я2 -9 = 0. Розв'язуємо квадратне рівняння й знаходимо власні числа:
Я2 - 12 Я + 11 = 0 ]^[Я = 1; Я = 11]
Знаходимо власні вектори:
Г х1 - 3х2 = 0 Г х1 - 3х2 = 0 Я = 1: і ^ і
1-3х1 + 9х2 = 0 І -х1 + 3х2 = 0
Для визначення сталої С1 запишемо вираз для довжини вектора у1 через його координати і прирівняємо його до одиниці, як це потрібно у постановці задачі ортогонального перетворення:

| 3х1 + х2 — 0 -3х1 - х2 — 0
|
■Г 1 Л
| С+ () — С1 — С1 —А-. у1 — А-
|
V 2 /О І о І 1
>/10
10
Я — 11:
Аналогічно знаходимо С2 і у2:
|у 2 І — С 2 V 12 +(-3)2 —Л0с2 — 1 ^ С2 ^ ^/Ю.
л/10
Одержуємо невироджене лінійне перетворення: у1 —-------- (3х1 + х2),
(хсі 3 Х2).
При зазначеному невиродженому лінійному перетворенні первинна квадратична форма набуде канонічного вигляду:
Ь1 (іУ)= уі2 + 11 • У 2 '
| Перевірка: уГ2 +11 • у. = 1
|
6 - 66
— (9 Х1 6 Х1Х2 х>2) ++ (Х1 6 Х1Х2 9 Х2) — Х1 Хі Хо Х2 —
10
10у 1 12 2/ 10
3.29. Індивідуальне завдання № 3.8
Студент повинен розв'язати одну з наведених нижче задач, вибравши її за своїм номером у журналі групи.
Звести квадратичну форму Ь (х1,х2) до канонічного вигляду методом Лагранжа й ортогональним перетворенням.
| 1.
| 3x1 2 Х1Х2 2 х^г
| 2.
| 2 Хl 2 ХlХ2 2 x..
| | 3.
| 2 Х1 2 Х1Х2 2 Х2
| 4.
| 3x1 4 ХlХ2 3x22
| | 5.
| 4 Х1 2 Х1Х2 5 Х2
| 6.
| 6 Хl 4 Хl Х2 x.J
| | 7.
| 4 Х1 2 Х1Х2 4 Х2
| 8.
| 3x1 2 Хl Х2 4 x..
| | 9.
| 3x1 2 Х1Х2 3x2
| 10.
| 8 Хl 4 Хl Х2 4 x..
| | 11.
| 3x1 2 Х1Х2 2 Х2
| 12.
| 4 Хl 6 ХlХ2 8 x..
| | 13.
| 6 Х1 4 Х1Х2 8 х>2
| 14.
| 4 Хl 4 ХlХ2 6 Х2
| | 15.
| 2 Х1 5 Х1Х2 4 Х2
| 16.
| 4 Хl 4 ХlХ2 2 x..
| | 17.
| 3x1 6 Х1Х2 4 Х2
| 18.
| 3x1 4 ХlХ2 3x22
| | 19.
| 5 Хl 8 Хl Х2 5 Х2
| 20.
| 4 Хl 6 ХlХ2 6 x..
| | 21.
| 3x1 4 Хl Х2 5 x.J
| 22.
| 2 Хl 8 Хl Х2 10 x.J
| | 23.
| 4 Хl 2 Хl Х2 3x22
| 24.
| 6 Хl 6 Хl Х2 4 x..
| | 25.
| 4 Хl 6 ХlХ2 5 x..
| 26.
| 4 Хl 4 ХlХ2 6 Х2
| | 27.
| 4 Хl 2 Хl Х2 4 Х2
| 28.
| 8 Хl 4 Хl Х2 4 x.J
| | 29.
| 6 Хl 4 ХlХ2 8 x.J
| 30.
| 3x1 4 ХlХ2 3x22
| | 31.
| 6 Хl 4 ХlХ2 Х2
|
|
| |
2 x]2 - 6 х1х2 +10 xC, ►