Скалярное произведение векторов в координатной форме.
Пусть Перемножая эти векторы как многочлены и учитывая вытекающие из равенств (3) и (6) соотношения
Таким образом, скалярное произведение двух векторов равно сумме парных произведений их одноименных координат Пример. Если
Отсюда с учетом формул (5) и (7) находим угол между векторами:
Задача. Найти расстояние между точками М1(х1; у1;z1),М2(х2; у2;, z2). Так как (см. § 2. 1, п. 8) В п. 1 было отмечено необходимое и достаточное условие opтогональности векторов в виде равенства (6). Согласно формуле (7) это условие можно представить в виде
|
и 
.
= 
= 
= 
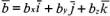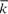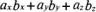.(7)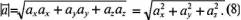
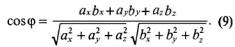
, то согласно формуле (8) 
.
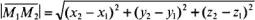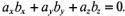(10)
