Скалярное произведение двух векторов и его основные свойства.
Определение. Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними. Скалярное произведение векторов
Через
т.е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось с направлением Раскроем физический смысл скалярного произведения. Если вектор A=| т.е. равна скалярному произведению векторов Скалярное произведение обладает следующими основными свойствами 1) 2) ( 3)( 4) ( Докажем, например, свойство 3. На основании формулы (2) и свойства проекций (см. § 2.1, (5)) имеем ( т.е. получаем равенство (4). Примечание. Из свойств 1, 3, 4 скалярного умножения и свойств линейных операций над векторами (см. § 2.1, п. 2) следует, что векторы можно перемножать скалярно как многочлены. Из равенства (1) следует, что косинус угла между двумя ненулевыми векторами
Из формулы (5) получаем, что два вектора
Это утверждение справедливо также и в том случае, когда хотя бы один из векторов
|

 и
и  обозначается символом
обозначается символом 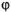 , то
, то обозначим проекцию вектора
обозначим проекцию вектора 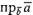 (см. § 2.1, п. 7), можно записать
(см. § 2.1, п. 7), можно записать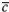 =
= 
 (
(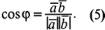
 тогда и только тогда, когда
тогда и только тогда, когда


