Базис на плоскости и в пространстве.
Определение. Базисом на плоскости называются два любых линейно независимых вектора. Из теоремы 2 (см. п. 4) следует, что два любых неколлинеарных вектора образуют базис. Пусть
Если вектор 1. Разложение вектора Доказательство. Допустим, что наряду с разложением (3) имеет место разложение
Покажем, что в этом случае
(Возможность почленного вычитания равенств (4) и (3) и производимой группировки членов вытекает из свойств линейных операций над векторами (см. п. 2).) Так как векторы базиса Определение. Базисом в пространстве называются три любых линейно независимых вектора. Из теоремы 2 (см. п. 5) следует, что три любых некомпланарных вектора образуют базис. Как и в случае плоскости, устанавливается, что любой вектор
причем это разложение единственное. Числа Основное значение базиса состоит в том, что линейные операции над векторами при задании базиса становятся обычными линейными операциями над числами - координатами этих векторов. Теорема. При сложении двух_векторов Доказательство. Пусть, например,
Тогда в силу свойств линейных операций (см. п. 2)
В силу единственности разложения по базису
|

 любой вектор на плоскости, а векторы
любой вектор на плоскости, а векторы  и
и  образуют базис. Так как на плоскости всякие три вектора линейно зависимы, то вектор
образуют базис. Так как на плоскости всякие три вектора линейно зависимы, то вектор  .
. и
и  называют координатами вектора
называют координатами вектора 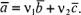
 Действительно, вычитая равенство (4) из равенства (3), получаем соотношение
Действительно, вычитая равенство (4) из равенства (3), получаем соотношение
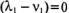 и
и  . Отсюда
. Отсюда  , т.е. разложение вектора
, т.е. разложение вектора  и
и 
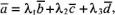
 называют координатами вектора
называют координатами вектора 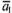 и
и 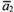 их координаты (относительно любого базиса
их координаты (относительно любого базиса  .
.



