Понятие линейной зависимости векторов.
Векторы
Векторы Из равенства (2), предполагая, например, что
Полагая
Выражение Таким образом, если несколько векторов линейно зависимы, то хотя бы один из них всегда можно представить в виде линейной комбинации остальных. Справедливо и обратное утверждение, если один из векторов представлен в виде линейной комбинации остальных векторов, то все эти векторы линейно зависимы.
4. Линейная зависимость векторов на плоскости. Теорема1. Всякие три вектора Доказательство
Достаточно убедиться в том, что один из векторов является линейной комбинацией остальных. Возможны два случая. 1. Среди данных векторов имеется пара
т.е. вектор 2.Среди данных векторов нет ни одной пары коллинеарных. Допустим, что все три вектора имеют общее начало О (рис.30). Покажем, что вектор Для этого через конец М вектора
Так как векторы Поэтому Следствие. Если число данных векторов на плоскости больше трех, то они также линейно зависимы. В самом деле, пусть даны n векторов
т.е. вектор Что касается двух векторов Теорема 2. Для того чтобы два вектора Из теорем 1 и 2 следует, что максимальное число линейно независимых векторов на плоскости равно двум.
|

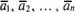 называются линейно зависимыми если существуют
называются линейно зависимыми если существуют  не все равные нулю, для которых имеет место
не все равные нулю, для которых имеет место
 .
. , получаем
, получаем
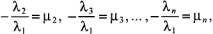

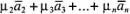 называется линейной комбинацией векторов
называется линейной комбинацией векторов ,
,  и
и  на плоскости линейно зависимы.
на плоскости линейно зависимы.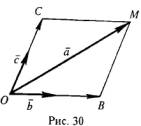
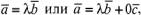
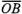 и
и  коллинеарны соответственно векторам
коллинеарны соответственно векторам 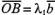 и
и  .
. , т.е.
, т.е. 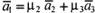 . В таком случае для всех n векторов можно написать
. В таком случае для всех n векторов можно написать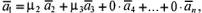
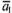 есть линейная комбинация остальных векторов.
есть линейная комбинация остальных векторов. , т.е. когда векторы
, т.е. когда векторы 


