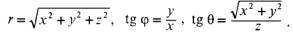В цилиндрической системе координат положение точки М пространства определяется полярными координатами r и 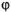 точки М' - проекции точки М на плоскость хОу - и аппликатой z самой точки М (рис. 38). Числа r,
точки М' - проекции точки М на плоскость хОу - и аппликатой z самой точки М (рис. 38). Числа r, 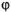 и z называются цилиндрическими координатами точки М, причем r
и z называются цилиндрическими координатами точки М, причем r 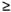 0, 0
0, 0 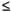
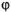 < 2
< 2 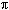 и z- любое действительное число. Из рис. 38 видно, что цилиндрические координаты r,
и z- любое действительное число. Из рис. 38 видно, что цилиндрические координаты r, 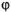 и z связаны с прямоугольными соотношениями
и z связаны с прямоугольными соотношениями
х = r cos 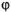 , у = r sin
, у = r sin 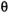 , z = z.
, z = z.
Рис.38
В сферической системе координат положение точки М в пространстве определяется ее расстоянием r от начала О, углом 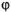 между положительным направлением оси Ох и проекцией отрезка ОМ на плоскость хОу, углом
между положительным направлением оси Ох и проекцией отрезка ОМ на плоскость хОу, углом 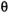 между положительным направлением оси Oz и отрезком ОМ (рис. 39). Числа r,
между положительным направлением оси Oz и отрезком ОМ (рис. 39). Числа r, 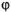 и
и 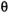 называются сферическими координатами точки М или полярными координатами в пространстве, при этом
называются сферическими координатами точки М или полярными координатами в пространстве, при этом
r 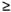 0, 0
0, 0 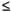
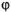 < 2
< 2 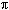 , 0
, 0 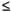
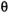
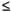
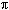 .
.
Из рис. 39 видно, что сферические координаты r, 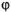 и
и 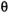 связаны с прямоугольными координатами соотношениями
связаны с прямоугольными координатами соотношениями
х =r sin 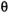 cos
cos 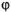 , у = r sin
, у = r sin 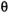 -sin
-sin 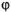 , z = r cos
, z = r cos 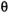 .
.
Откуда
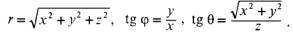

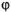 точки М' - проекции точки М на плоскость хОу - и аппликатой z самой точки М (рис. 38). Числа r,
точки М' - проекции точки М на плоскость хОу - и аппликатой z самой точки М (рис. 38). Числа r, 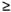 0, 0
0, 0 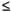
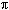 и z- любое действительное число. Из рис. 38 видно, что цилиндрические координаты r,
и z- любое действительное число. Из рис. 38 видно, что цилиндрические координаты r, 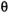 , z = z.
, z = z.