Определение. Векторным произведением двух векторов  и
и  называется новый вектор
называется новый вектор 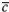 , модуль которого равен площади параллелограмма, построенного на векторах
, модуль которого равен площади параллелограмма, построенного на векторах  и
и  , приведенных к общему началу, и который перпендикулярен к перемножаемым векторам (иначе говоря, перпендикулярен к плоскости построенного на них параллелограмма) и направлен в такую сторону, чтобы кратчайший поворот от
, приведенных к общему началу, и который перпендикулярен к перемножаемым векторам (иначе говоря, перпендикулярен к плоскости построенного на них параллелограмма) и направлен в такую сторону, чтобы кратчайший поворот от  к
к  вокруг полученного вектора
вокруг полученного вектора 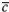 представлялся происходящим против часовой стрелки, если смотреть из конца вектора
представлялся происходящим против часовой стрелки, если смотреть из конца вектора 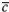 (рис. 40).
(рис. 40).

Если векторы  и
и  коллинеарны, то их векторное произведение считается равным нулевому вектору. Из этого определения следует, что
коллинеарны, то их векторное произведение считается равным нулевому вектору. Из этого определения следует, что
| 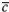 | = |
| = |  | |
| |  | sin
| sin 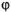 ,
,
где 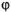 - угол между векторами
- угол между векторами  и
и  (0
(0 
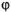

 ). Векторное произведение векторов
). Векторное произведение векторов  и
и  обозначается символом
обозначается символом
 х
х  или [
или [ 
 ] или [
] или [  ,
,  ].
].
Выясним физический смысл векторного произведения. Если вектор  изображает приложенную в некоторой точке М с илу, а вектор
изображает приложенную в некоторой точке М с илу, а вектор  идет из некоторой точки О в точку М, то вектор
идет из некоторой точки О в точку М, то вектор 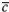 = [
= [ 
 ] представляет собой момент силы
] представляет собой момент силы  относительно точки О.
относительно точки О.
Свойства векторного произведения
1. При перестановке сомножителей векторное произведение меняет знак, т.е.
 х
х  = -(
= -( x
x  ).
).
2.
(
 )х
)х  =
=  х(
х(
 )=
)=  (
( х
х  ), где
), где  - скаляр.
- скаляр.
3. Векторное произведение подчиняется распределительному закону, т.е.
( +
+  ) x
) x 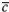 =
=  x
x 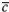 +
+  x
x 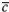 .
.
4. Если векторное произведение двух векторов равно нулевому вектору, то либо равен нулевому вектору хотя бы один из перемножаемых векторов (тривиальный случай), либо равен нулю синус угла между ними, т.е. векторы коллинеарны.
Обратно, если два ненулевых вектора коллинеарны, то их векторное произведение равно нулевому вектору.
Таким образом, для того чтобы два ненулевых вектора  и
и  были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
Отсюда, в частности, следует, что векторное произведение вектора на самого себя равно нулевому вектору:
 х
х  = 0
= 0
( х
х  еще называют векторным квадратом вектора
еще называют векторным квадратом вектора  .
.

 и
и  называется новый вектор
называется новый вектор 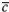 , модуль которого равен площади параллелограмма, построенного на векторах
, модуль которого равен площади параллелограмма, построенного на векторах 
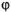 ,
,
 ). Векторное произведение векторов
). Векторное произведение векторов 



