Властивості центрального проеціювання
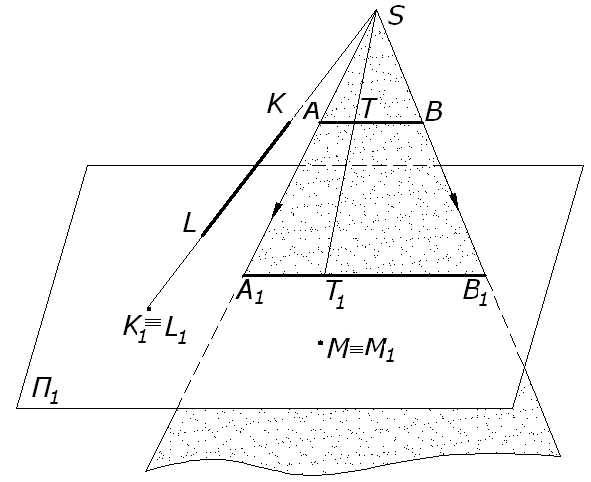
1. Проекція точки – точка. Якщо точка М належить площині П1, то точка М º М1 (збігається) з своєю проекцією. 2. Проекція відрізка – відрізок, крім тих випадків, коли відрізок (пряма) співпадає з проеціюючим променем. [AB]®П1 = [A1 B1], [Kt]®П1 = K1t1 (точка), рис. 1.2.
Рис. 1.2
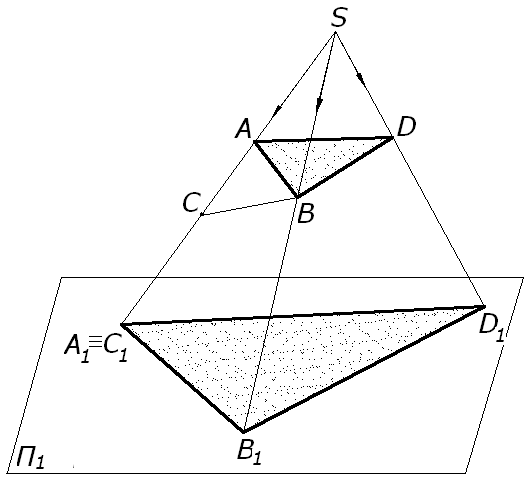
3. Проекція плоскої фігури – плоска фігура. Крім тих випадків, коли плоска фігура лежить у проеціюючій площині. êABD®П1 = êA1B1D1, êABC®П1 = [A1B1], рис. 1.3.
Рис. 1.3
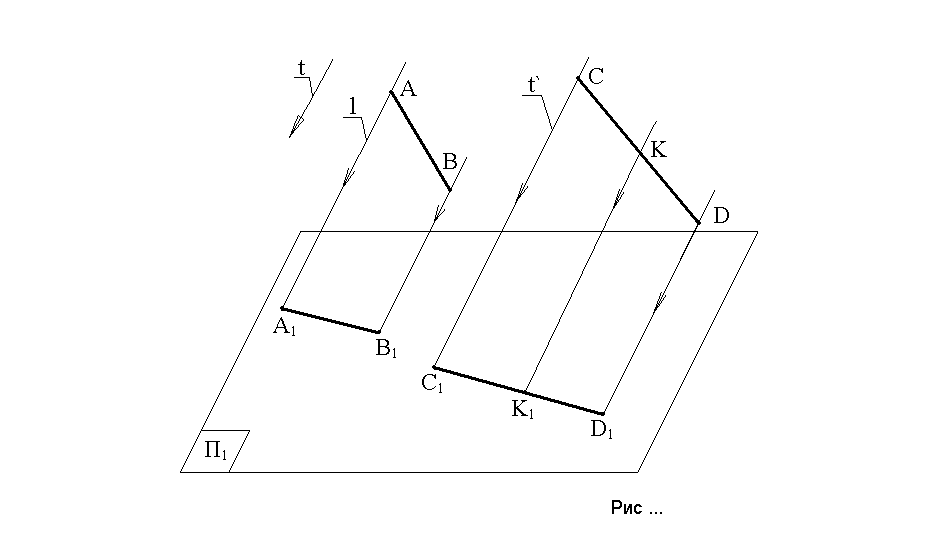
4. При центральному проеціюванні зберігається приналежність геометричних фігур. Якщо ТÌ(АВ), то Т1Ì(А1В1), рис. 1.2. 5. Проекція просторової фігури – плоска фігура. 6. Проекції плоскої (просторової) фігури на паралельні площини – подібні. Зображення, що їх отримують при центральному проеціюванні, наочні, але складні в побудові і без додаткових умов не є вимірюваними. За принципом центрального проеціювання працює кінокамера, функціонує око. Цей спосіб використовують при побудові наочних зображень у архітектурно-будівельній справі, малюванні. Паралельне проеціювання можна вважати окремим випадком центрального проеціювання, коли центр проекцій точка S знаходиться нескінченно далеко, тобто всі проеціюючі промені паралельні між собою. Апаратом паралельного проеціювання є напрямок проеціювання (пряма t) та площина П1 (площина проекцій) рис. 1.4.
Рис. 1.4
Для отримання, наприклад паралельної проекції точки А необхідно через точку А провести проеціюючий промінь t’, що паралельний t. Знайти точку перетину променя t з площиною П1. Точка перетину (А1) і буде проекцією точки А. Скорочено можна записати так: 1. А Ì t, t’j t. 2. t’ I П1 = A1 A ® П1 = A1
|