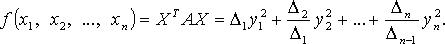Определения квадратичной формы, матрицы квадратичной формы, канонического вида квадратичной формы.Квадратичной формой Обозначая коэффициент при
Симметричная матрица Пример. Написать матрицу квадратичной формы
Здесь Следовательно,
В векторно-матричной форме квадратичная форма имеет вид
Если в квадратичной форме
получится квадратичная форма Канонический вид квадратичной формы
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы. 1. Ортогональное преобразование пространства
где 2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если
Затем подобную процедуру проделывают с квадратичной формой 3. Метод Якоби (в случае, когда все главные миноры
|
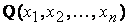от n неизвестных 
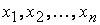называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных.
через 
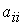, а при произведении 
– через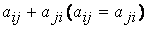 
, квадратичную форму Q можно представить в виде
.
называется матрицей квадратичной формы Q.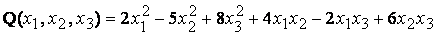
.
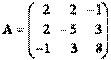
A 
, где 
А 
неизвестные подвергнуть линейному преобразованию 
, где 
,
с матрицей 
.
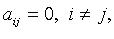т. е.
:
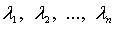- собственные значения матрицы A.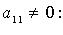
и т. д. Если в квадратичной форме все 
но есть 
то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например, 
то полагаем 
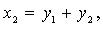
квадратичной формы отличны от нуля):
