Метод Лагранжа приведения квадратичной формы к каноническому виду.
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть
есть данная квадратичная форма. Возможны два случая: хотя бы один из коэффициентов при квадратах отличен от нуля. Не нарушая общности, будем считать (этого всегда можно добиться соответствующей перенумерацией переменных); все коэффициенты, но есть коэффициент, отличный от нуля (для определённости пусть будет). В первом случае преобразуем квадратичную форму следующим образом:
С ней поступают аналогичным образом и так далее. Заметим, что Второй случай заменой переменных
|
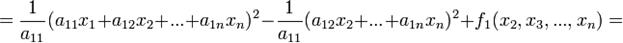
, где
, а через 
обозначены все остальные слагаемые.
представляет собой квадратичную форму от n-1 переменных. 
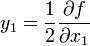
сводится к первому.
