Тест ПаркаТест Парка основан на предположении, что дисперсия
где
Выдвигаются гипотеза Условие принятия гипотезы Если данное условие выполняется, то гипотеза о наличии гетероскедастичности будет принята при уровне значимости Пример 3.2. Проверим гипотезу о гетероскедастичности остатков с помощью теста Парка для данных из примера 3.1. Зависимость между остаточной дисперсией и объясняющим фактором имеет вид:
Табличное значение критерия Стьюдента равно Поскольку условие
|
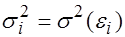является функцией 
-го значения объясняющей переменной 
. Парк предложил следующую зависимость.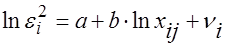
,
— 
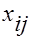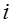-е значение 
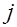-го фактора
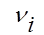— случайный остаток
, что соответствует гомоскедастичности остатков, и гипотеза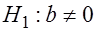 
, которая выявляет наличие связи между 
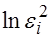и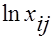 
. Отсюда следует, что гетероскедастичность остатков имеет место.
: 
.
.
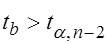
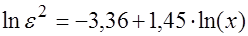
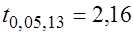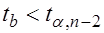выполняется, то гипотеза о наличии гетероскедастичности отклоняется.
