Методы устранения гетероскедастичности
При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный метод наименьших квадратов (известный в английской терминологии как метод OLS – Ordinary Least Squares) заменять обобщенным методом, т.е. методом GLS (Generalized Least Squares). Применение обычного МНК к модели, в которой нарушены эти предпосылки, ведет к тому, что найденные параметры уравнения регрессии не будут эффективными оценками генеральных параметров. Кроме того, их дисперсии будут рассчитаны со смещением, что приведет к ложным выводам при оценке качества модели и при проведении прогнозирования по ней. Для случая гетероскедастичности остатков обобщенный метод наименьших квадратов (ОМНК) называют еще методом взвешенных наименьших квадратов (ВМНК). ОМНК используется для корректировки гетероскедастичности, за счет преобразования данных, позволяющего получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Пусть
Тогда дисперсия остатков представляется в виде:
В результате этой процедуры каждое наблюдение будет иметь случайную ошибку с единичной дисперсией. Следовательно, для преобразованной модели выполняется предпосылка МНК о гомоскедастичности дисперсии остатков, а оценки параметров регрессии, полученные по МНК, будут наилучшими несмещенными оценками. Применение вышеописанного метода в значительной степени ограничено тем, что на практике фактические значения
При этом в отношении величин Тогда уравнение
В данной модели остаточные величины гетероскедастичны, следовательно для регрессии применим обычный МНК. Действительно, в силу выполнимости предпосылки
Оценка параметров нового уравнения с преобразованными переменными основана на минимизации суммы квадратов отклонений вида
Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Например, рассматривается модель вида
для которой дисперсия остаточных величин оказалась пропорциональна
для корректировки гетероскедастичности выполняется переход к уравнению с новым преобразованным переменным:
Параметры такой модели зависят от концепции, принятой для коэффициента пропорциональности
предположить, что
Таким образом «взвешивая» каждый остаток
|

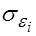 — стандартное отклонение случайной ошибки
— стандартное отклонение случайной ошибки  в
в  –м наблюдении. В случае если
–м наблюдении. В случае если  соответствующее преобразование данных будет иметь вид:
соответствующее преобразование данных будет иметь вид: .
.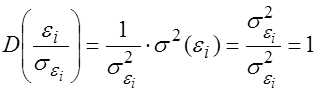
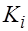 на постоянную величину
на постоянную величину  :
: .
.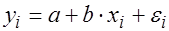 преобразуется к виду:
преобразуется к виду: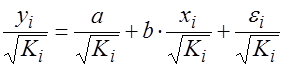 .
. имеем:
имеем:
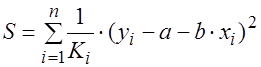 и последующего решения системы уравнений:
и последующего решения системы уравнений: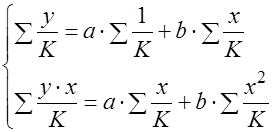 .
. ,
, . Коэффициент пропорциональности
. Коэффициент пропорциональности 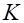 принимает различные значения для соответствующих
принимает различные значения для соответствующих  значений факторов
значений факторов 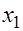 и
и  . Ввиду того, что
. Ввиду того, что ,
,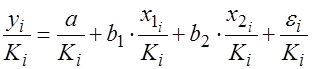 .
.
 и
и  , то ОМНК предполагает оценку параметров следующего трансформированного уравнения:
, то ОМНК предполагает оценку параметров следующего трансформированного уравнения: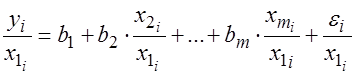 .
.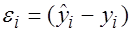 с помощью коэффициента
с помощью коэффициента 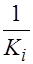 , можно добиться равномерного вклада остатков в общую сумму, что приводит конечном итоге к получению наиболее эффективных оценок параметров регрессии. Вместе с тем, следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным.
, можно добиться равномерного вклада остатков в общую сумму, что приводит конечном итоге к получению наиболее эффективных оценок параметров регрессии. Вместе с тем, следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным.


