Тест Голдфельда-Квандта
Тест Голдфельда-Квандта применяется если случайные остатки предполагаются нормально распределенными случайными величинами и стандартное отклонение Процедура проверки состоит в следующем: 1. Все наблюдения упорядочиваются по возрастанию фактора 2. Упорядоченная совокупность разбивается на три группы размерностей 3. Оцениваются отдельные регрессии для первой группы ( 4. Формулируются: Основная гипотеза, предполагающая постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности: Альтернативная гипотеза, предполагающая непостоянство дисперсий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности: 5. Для сравнения соответствующих дисперсий вычисляется фактическое значение
Здесь Если Этот же тест может использоваться при предположении об обратной пропорциональности между
Для множественной регрессии данный тест обычно проводится для той объясняющей переменной, которая в наибольшей степени связана с Пример 3.3 Проверим гипотезу о гетероскедастичности остатков с помощью теста Гольдфельда-Квандта для данных из примера 3.1. 1. Данные таблицы 3.1 упорядочим по значению фактора Таблица 3.2
2. Определим значение 3. Оценим регрессии по первой и третьей группе данных.
4. Вычислим фактическое значение
Табличное значение критерия Фишера Поскольку условие
|

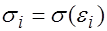 пропорционально значению
пропорционально значению 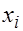 переменной
переменной  в этом наблюдении, т.е.
в этом наблюдении, т.е. 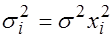 ,
, 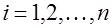 .
.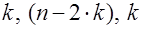 соответственно. Причем
соответственно. Причем 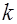 должно быть больше чем число параметров модели. Для парной регрессии Голдфельд и Квандт предлагают следующие пропорции:
должно быть больше чем число параметров модели. Для парной регрессии Голдфельд и Квандт предлагают следующие пропорции:  ;
; 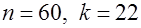 .
.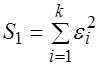 ) будет существенно меньше дисперсии регрессии по третьей группе (рассчитываемой как
) будет существенно меньше дисперсии регрессии по третьей группе (рассчитываемой как 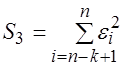 ).
).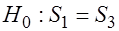 .
.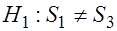
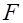 -критерия:
-критерия:
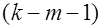 — число степеней свободы соответствующих выборочных дисперсий (
— число степеней свободы соответствующих выборочных дисперсий (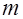 — количество объясняющих переменных в уравнении регрессии).
— количество объясняющих переменных в уравнении регрессии).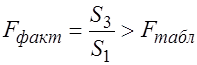 (где
(где 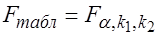 ,
,  – выбранный уровень значимости), то гипотеза
– выбранный уровень значимости), то гипотеза 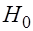 об отсутствии гетероскедастичности отклоняется.
об отсутствии гетероскедастичности отклоняется.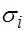 и значениями объясняющей переменной. При этом статистика Фишера имеет вид:
и значениями объясняющей переменной. При этом статистика Фишера имеет вид: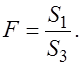
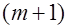 . Если нет уверенности относительно выбора переменной
. Если нет уверенности относительно выбора переменной 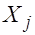 , то данный тест может осуществляться для каждой из объясняющих переменных.
, то данный тест может осуществляться для каждой из объясняющих переменных.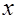 .
.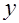 (тыс. шт.)
(тыс. шт.)
 .
.
 .
.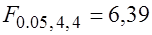 .
. выполняется, то гипотеза о наличии гетероскедастичности отклоняется.
выполняется, то гипотеза о наличии гетероскедастичности отклоняется.


