Модели регрессии с фиктивными переменными сдвига
Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для общей совокупности наблюдений уравнение регрессии имеет вид:
где Аналогичные уравнения могут быть найдены, если рассматривать отдельно потребление кофе для категории – лица мужского пола: Различия в потреблении кофе проявятся в различии средних
В этом случае зависимая переменная
Тогда уравнение для лиц женского пола можно записать: Сравнивая два полученных уравнения, видим, что они различаются величиной свободного члена. То есть для одного уровня неколичественной переменной уровень результата в среднем будет на
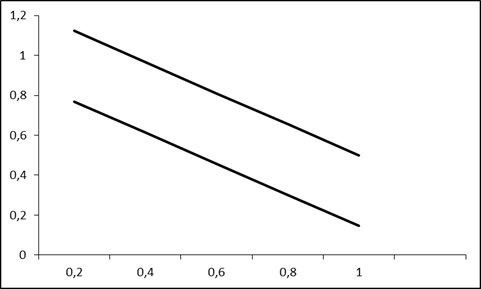
Рис 4.1 Модель регрессии с фиктивной переменной сдвига Если рассмотреть зависимость потребления кофе не только от цены, но и региона проживания: северные регионы, центральные и южные. В этом случае все данные разбиваются на три категории. В модель вводятся две фиктивные переменные
Значение Линейная регрессионную модель в этом случае определяется следующим уравнением:
где коэффициенты Таким образом, построение модели с фиктивными переменными требует выполнения следующих этапов: 1. Статистические данные разбиваются на категории, число которых определяется числом значений качественного признака. Одна из категорий принимается за эталонную (выбирается произвольно). 2. Вводятся фиктивные переменные для всех категорий, кроме эталонной. Каждая из введенных фиктивных переменных принимает значение, равное единице для данных рассматриваемой категории и нуль для данных остальных категорий. 3. Фиктивные переменные вводятся в уравнение с коэффициентом Модель может содержать несколько качественных признаков. В этом случае фиктивные переменные для каждого признака вводятся в соответствии с вышеприведенной методикой.
|

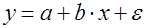 ,
,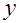 – количество потребляемого кофе;
– количество потребляемого кофе; 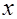 – цена.
– цена. и категории – лица женского пола:
и категории – лица женского пола:  .
.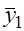 и
и  . Вместе с тем сила влияния
. Вместе с тем сила влияния 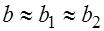 . Для построения общего уравнения регрессии, учитывающего различия в потреблении кофе мужчинами и женщинами, возможно включение в него фактора «пол» в виде фиктивной переменной.
. Для построения общего уравнения регрессии, учитывающего различия в потреблении кофе мужчинами и женщинами, возможно включение в него фактора «пол» в виде фиктивной переменной.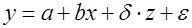 .
. . Переменная
. Переменная 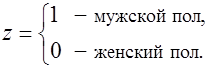
 , а для лиц мужского пола:
, а для лиц мужского пола: 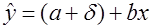 .
. единиц выше или ниже другого. Иными словами
единиц выше или ниже другого. Иными словами 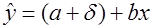
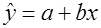
 и
и  :
:

 и
и  принимается за эталонное и определяет среднее значение потребления кофе проживающих в центральном регионе.
принимается за эталонное и определяет среднее значение потребления кофе проживающих в центральном регионе.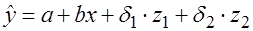 ,
, и
и  показывают сдвиг в объеме потребления кофе в соответствующих регионах по отношению к потреблению кофе в центральных регионах.
показывают сдвиг в объеме потребления кофе в соответствующих регионах по отношению к потреблению кофе в центральных регионах. ,
,  , где
, где 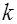 - число категорий. Каждый из коэффициентов
- число категорий. Каждый из коэффициентов  - ой категории относительно эталонной. Если
- ой категории относительно эталонной. Если 


