Исследование структурных изменений с помощью теста Чоу.
В практике эконометрических исследований нередки случаи, когда для выявления зависимости между показателями имеются выборки их значений, полученных при разных условиях. Необходимо выяснить, действительно ли две выборки однородны в регрессионном смысле. Другими словами, можно ли объединить две выборки в одну и рассматривать единую модель регрессии. При достаточных объемах выборок можно, например, построить интервальные оценки параметров регрессии по каждой из выборок и в случае пересечения соответствующих доверительных интервалов сделать вывод о единой модели регрессии. Возможны и другие подходы. В случае, если объем хотя бы одной из выборок незначителен, то возможности такого подхода резко сужаются из-за невозможности построения регрессии с достаточно надежными оценками. Для проверки возможности объединения выборок в одну можно использовать тест Чоу. Алгоритм теста Пусть имеется две подвыборки: одна объемом 1. По каждой подвыборке строятся линейные регрессионные модели с
Рассчитываются суммы квадратов остатков для этих регрессий 2. Строится линейная регрессия по объединенной выборке:
Вычисляется ее сумма квадратов остатков 3. Формулируется нулевая гипотеза:
Очевидно, что при совпадении параметров регрессии выполняется равенство 4. Для проверки гипотезы вычисляется фактическое значение
Здесь В случае, если Если, Пример 4.3. Используем тест Чоу для выявления целесообразности рассмотрения общей выборки и введения фиктивной переменной на примере данных предыдущего параграфа, выделив две подвыборки: ( Таблица 4.6 Изменение заработной платы мужчин в зависимости от стажа
Таблица 4.7 Изменение заработной платы женщин в зависимости от стажа.
Построим по каждой из них линейные модели зависимости заработной платы (
Построим линейную модель по объединенной выборке:
Рассчитаем статистику
|

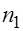 , а другая объемом
, а другая объемом 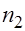 .
. переменными:
переменными: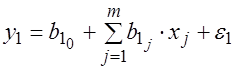 , для первой подвыборки,
, для первой подвыборки, , для второй подвыборки.
, для второй подвыборки.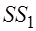 и
и 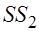 .
.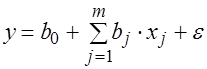 .
.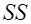 .
.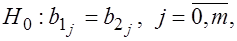 где
где 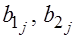 — параметры моделей.
— параметры моделей.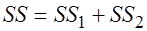 . Чем сильнее различие в поведении
. Чем сильнее различие в поведении 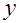 для двух подвыборок, тем больше значение
для двух подвыборок, тем больше значение 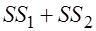 .
.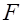 -статистики по формуле:
-статистики по формуле: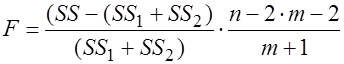 .
.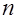 — число наблюдений по всей совокупности.
— число наблюдений по всей совокупности.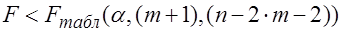 , то считается, что различие между
, то считается, что различие между 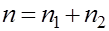 .
.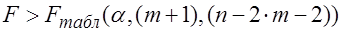 то различие между
то различие между  ) и (
) и (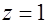 ).
).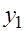
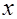
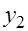
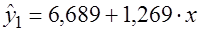 ;
;  ;
;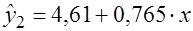 ;
;  .
.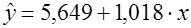 ;
; 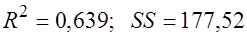 .
.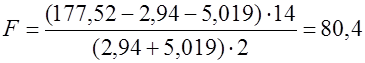 .
.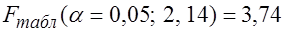 . Так как вычисленное значение
. Так как вычисленное значение 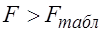 , то следует признать существенность различия роста заработной платы от стажа в зависимости от пола. Следовательно, для построения общего уравнения регрессии целесообразно ввести фиктивную переменную, определяющую пол работника, что и показано в примере предыдущего параграфа.
, то следует признать существенность различия роста заработной платы от стажа в зависимости от пола. Следовательно, для построения общего уравнения регрессии целесообразно ввести фиктивную переменную, определяющую пол работника, что и показано в примере предыдущего параграфа.


