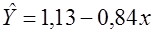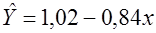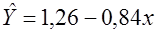Пример 4.1.
Предположим, что изучается потребление кофе в зависимости от цены, пола и региона проживания: северные регионы, центральные и южные (таблица 4.1).
Таблица 4.1
|
N
| Потребл. (кг)
| Цена (тыс. руб)
| Пол
| Cеверн. регион
| Южн. регион
|
N
| Потребл. (кг)
| Цена (тыс. руб)
| Пол
| Cеверн. регион
| Южн. регион
| | Y
| 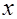
| 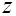
| 
| 
| Y
| 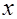
| 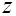
| 
| 
| |
| 0,2
|
|
|
|
|
| 0,6
| 0,6
|
|
|
| |
| 0,4
|
|
|
|
|
| 0,6
| 0,5
|
|
|
| |
| 0,4
| 0,8
|
|
|
|
| 0,65
| 0,5
|
|
|
| |
| 0,6
| 0,8
|
|
|
|
| 0,6
| 0,3
|
|
|
| |
| 0,6
| 0,6
|
|
|
|
| 0,7
| 0,3
|
|
|
| |
| 0,8
| 0,6
|
|
|
|
| 0,5
|
|
|
|
| |
| 0,75
| 0,5
|
|
|
|
| 0,6
|
|
|
|
| |
| 0,9
| 0,5
|
|
|
|
| 0,7
| 0,8
|
|
|
| |
| 0,9
| 0,3
|
|
|
|
| 0,9
| 0,8
|
|
|
| |
| 1,1
| 0,3
|
|
|
|
| 0,9
| 0,6
|
|
|
| |
| 0,2
|
|
|
|
|
| 1,1
| 0,6
|
|
|
| |
| 0,45
|
|
|
|
|
|
| 0,5
|
|
|
| |
| 0,45
| 0,8
|
|
|
|
| 1,2
| 0,5
|
|
|
| |
| 0,6
| 0,8
|
|
|
|
| 1,2
| 0,3
|
|
|
| |
| 0,5
| 0,6
|
|
|
|
| 1,4
| 0,3
|
|
|
|
Вводим фиктивную бинарную переменную 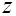 для признака «пол» и две бинарные переменные для признака «пол» и две бинарные переменные  и и  для регионов проживания. для регионов проживания.
Линейная регрессионная модель запишется:
 . .
Коэффициент  показывает сдвиг в потреблении кофе мужчинами относительно женщин, а коэффициенты показывает сдвиг в потреблении кофе мужчинами относительно женщин, а коэффициенты  и и  соответственно показывают сдвиг в объеме потребления кофе в северных и южных регионах относительно центрального региона. После вычисления коэффициентов уравнение регрессии имеет вид: соответственно показывают сдвиг в объеме потребления кофе в северных и южных регионах относительно центрального региона. После вычисления коэффициентов уравнение регрессии имеет вид:
  . .
Коэффициент детерминации 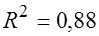 , что говорит о хорошем качестве модели. Статистическая значимость модели в целом подтверждается значением критерия Фишера , что говорит о хорошем качестве модели. Статистическая значимость модели в целом подтверждается значением критерия Фишера 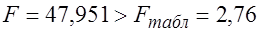 . .
Оценка значимости коэффициентов регрессии выполняется на основе анализа следующих величин (таблица 4.2):
Таблица 4.2
|
| Значения коэффициентов
| Стан. ошибка
| t-стат.
| P-Значение
| 
| 1,26
| 0,07
| 19,26
| 1,64Е-16
| 
| -0,84
| 0,08
| -10,30
| 1,77Е-10
| 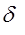
| -0,11
| 0,04
| -2,88
| 0,008
| 
| -0,13
| 0,05
| -2,70
| 0,012
| 
| 0,29
| 0,05
| 5,91
| 3,63Е-0,6
| Так как расчетные значения  -статистики для всех коэффициентов по модулю превышают табличное значение -статистики для всех коэффициентов по модулю превышают табличное значение  , то они статистически значимы. Следовательно, потребление кофе существенно зависит от цены, пола и проживания в определенном регионе. , то они статистически значимы. Следовательно, потребление кофе существенно зависит от цены, пола и проживания в определенном регионе.
Можно построить отдельные уравнения для мужчин и женщин и каждого региона (таблица 4.3).
Таблица 4.3
| Тип категории
| уравнение
| | Женщины (северные регионы)
| 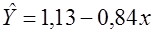
| | Мужчины (северные регионы)
| 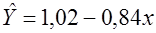
| | Женщины (центральные регионы)
| 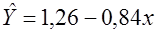
| | Мужчины (центральные регионы)
| 
| | Женщины (южные регионы)
| 
| | Мужчины (южные регионы)
| 
| В этих уравнениях различны только свободные члены, угол наклона всех прямых одинаков (одинаковый коэффициент перед переменной «цена»).

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
РЕВМАТИЧЕСКИЕ БОЛЕЗНИ Ревматические болезни(или диффузные болезни соединительно ткани(ДБСТ))— это группа заболеваний, характеризующихся первичным системным поражением соединительной ткани в связи с нарушением иммунного гомеостаза...
Решение Постоянные издержки (FC) не зависят от изменения объёма производства, существуют постоянно...
ТРАНСПОРТНАЯ ИММОБИЛИЗАЦИЯ
Под транспортной иммобилизацией понимают мероприятия, направленные на обеспечение покоя в поврежденном участке тела и близлежащих к нему суставах на период перевозки пострадавшего в лечебное учреждение...
|
Гальванического элемента При контакте двух любых фаз на границе их раздела возникает двойной электрический слой (ДЭС), состоящий из равных по величине, но противоположных по знаку электрических зарядов...
Сущность, виды и функции маркетинга персонала Перснал-маркетинг является новым понятием. В мировой практике маркетинга и управления персоналом он выделился в отдельное направление лишь в начале 90-х гг.XX века...
Разработка товарной и ценовой стратегии фирмы на российском рынке хлебопродуктов В начале 1994 г. английская фирма МОНО совместно с бельгийской ПЮРАТОС приняла решение о начале совместного проекта на российском рынке. Эти фирмы ведут деятельность в сопредельных сферах производства хлебопродуктов.
МОНО – крупнейший в Великобритании... |
|

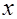
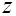


 .
. показывает сдвиг в потреблении кофе мужчинами относительно женщин, а коэффициенты
показывает сдвиг в потреблении кофе мужчинами относительно женщин, а коэффициенты  и
и  соответственно показывают сдвиг в объеме потребления кофе в северных и южных регионах относительно центрального региона. После вычисления коэффициентов уравнение регрессии имеет вид:
соответственно показывают сдвиг в объеме потребления кофе в северных и южных регионах относительно центрального региона. После вычисления коэффициентов уравнение регрессии имеет вид:
 .
.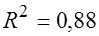 , что говорит о хорошем качестве модели. Статистическая значимость модели в целом подтверждается значением критерия Фишера
, что говорит о хорошем качестве модели. Статистическая значимость модели в целом подтверждается значением критерия Фишера 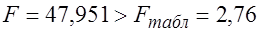 .
.

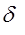

 -статистики для всех коэффициентов по модулю превышают табличное значение
-статистики для всех коэффициентов по модулю превышают табличное значение  , то они статистически значимы. Следовательно, потребление кофе существенно зависит от цены, пола и проживания в определенном регионе.
, то они статистически значимы. Следовательно, потребление кофе существенно зависит от цены, пола и проживания в определенном регионе.