Предпосылки МНК
Глава 3 Гетероскедастичность и автокорреляция остатков Предпосылки МНК В задачу практического регрессионного анализа входит получение качественных оценок параметров уравнения регрессии. Качество оценок параметров определяется свойствами: несмещенность, состоятельность и эффективность. Несмещенность оценки параметра означает, что ее математическое ожидание равно оцениваемому параметру:
где
Оценка параметра является эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок данного параметра по выборкам одного и того же объема:
Оценка параметра является состоятельной, если с увеличением числа наблюдений оценка параметра стремится к ее значению в генеральной совокупности.
Перечисленные свойства оценок параметров имеют чрезвычайно важное практическое значение в использовании результатов регрессии и обязательно учитываются при разных способах оценивания. МНК строит оценки регрессионной модели на основе минимизации суммы квадратов остатков, поэтому их свойства напрямую зависят от свойств случайной составляющей В модели
случайная составляющая
Исследование остатков 1) случайный характер остатков 2) нулевая средняя величина остатков, не зависящая от 3) гомоскедастичность — дисперсия каждого отклонения 4) отсутствие автокорреляции остатков – значения остатков 5) остатки подчиняются нормальному распределению. Если распределение случайных остатков Проверка первой предпосылки МНК о случайном характере остатков
Рис. 3.1 Зависимость случайных остатков от теоретических значений Проверка второй предпосылки МНК относительно нулевой средней величины остатков независящей от В рамках соблюдения второй предпосылки МНК также исследуется независимость случайных остатков и величины
Рис. 3.2 Зависимость величины остатков от величины фактора Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений · нарушение третьей предпосылки МНК. · неправильная спецификация модели и в нее необходимо ввести дополнительные члены от · наличие систематической погрешности модели, что отражается скоплением точек в определенных участках значений фактора Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений. Это значит, что для каждого значения фактора При невыполнимости предпосылки постоянства дисперсий отклонений последствия применения МНК будут следующими. 1. Оценки коэффициентов по-прежнему останутся несмещенными и линейными. 2. Оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок. 3. Дисперсии оценок будут рассчитываться со смещением. 4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих Обнаружение гетероскедастичности дисперсии остатков может быть выполнено различными методами. К настоящему времени разработано большое число тестов и критериев для них. Наиболее популярные из них: графический анализ остатков, тест ранговой корреляции Спирмена, тест Парка, Тест Голдфелда-Квандта. При построении регрессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т.е. значения остатков
т.е. по обычной формуле линейного коэффициента корреляции. Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированы и функция плотности вероятности точки наблюдения и от распределения значений остатков в других точках наблюдения. Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии. Особенно актуально соблюдение данной предпосылки МНК при построении регрессионных моделей по рядам динамики, где ввиду наличия тенденции последующие уровни динамического ряда, как правило, зависят от своих предыдущих уровней. Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью
|

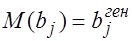 ,
,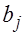 — оценка параметра;
— оценка параметра;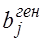 — значение параметра в генеральной совокупности.
— значение параметра в генеральной совокупности.

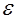 .
.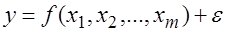
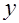 :
: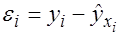
 предполагает проверку выполнения пяти предпосылок МНК:
предполагает проверку выполнения пяти предпосылок МНК: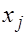 ;
;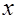 ;
; не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
не соответствует некоторым предпосылкам МНК, то следует корректировать модель. хорошо аппроксимируют фактические значения
хорошо аппроксимируют фактические значения 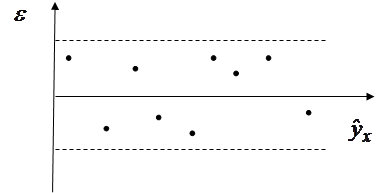
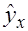 .
.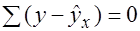 . Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.
. Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.
 .
.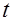 - и
- и 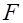 - статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно,
- статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно, 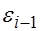 , где
, где  ,
,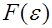 зависит от
зависит от  -й
-й


