Система ненулевых векторов 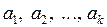 линейного пространства
линейного пространства  называется линейно зависимой, если существуют числа
называется линейно зависимой, если существуют числа  , среди которых есть хотя бы одно отличное от нуля, причем выполняется равенство
, среди которых есть хотя бы одно отличное от нуля, причем выполняется равенство
 . (1.1)
. (1.1)
Система ненулевых векторов 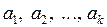 линейного пространства
линейного пространства  называется линейно независимой, если равенство (1.1) выполняется только при всех значениях
называется линейно независимой, если равенство (1.1) выполняется только при всех значениях  , равных нулю одновременно.
, равных нулю одновременно.
Если система векторов 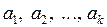 – линейно зависима, то хотя бы один вектор
– линейно зависима, то хотя бы один вектор  есть линейная комбинация остальных векторов:
есть линейная комбинация остальных векторов:
 .
.
Задание 2. Исследовать на линейную зависимость систему векторов  . В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы.
. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы.
2.1.  ,
,  ,
,  ,
, 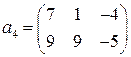 .
.
2.2. 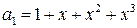 ,
,  ,
, 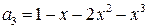 ,
,
 .
.
2.3.  ,
, 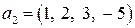 ,
, 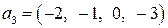 ,
,
 .
.
2.4.  ,
,  ,
,  ,
,
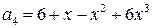 .
.
2.5.  ,
,  ,
,  ,
,  .
.
2.6.  (3, –4, 1, 2),
(3, –4, 1, 2),  (1, –1, –1, –1),
(1, –1, –1, –1), 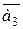 (4, –3, 1, 2),
(4, –3, 1, 2), 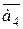 (1, –6, 1, 2).
(1, –6, 1, 2).
2.7.  (1, –1, 2, –1),
(1, –1, 2, –1),  (2, 3, –1, 2),
(2, 3, –1, 2), 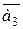 (4, 1, 3, 1),
(4, 1, 3, 1), 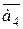 (–1, –9, 8, –7).
(–1, –9, 8, –7).
2.8.  ,
,  ,
, 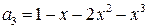 ,
,
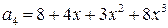 .
.
2.9. 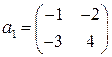 ,
,  ,
,  ,
,  .
.
2.10.  ,
, 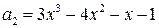 ,
,  ,
,
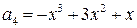 .
.
2.11.  .
.
2.12.  ,
,  ,
,  ,
,
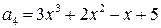 .
.
2.13.  ,
,  ,
,  ,
,
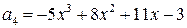 .
.
2.14. 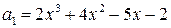 ,
, 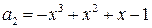 ,
,  ,
,
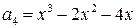 .
.
2.15.  (4, 3, –1, 1),
(4, 3, –1, 1),  (2, 1, –3, 2),
(2, 1, –3, 2), 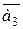 (1, –3, 0, 1),
(1, –3, 0, 1), 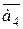 (1, 5, 2, –2).
(1, 5, 2, –2).
2.16.  ,
,  ,
, 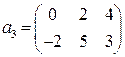 ,
, 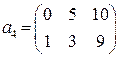 .
.
2.17.  ,
,  ,
,  ,
,
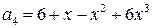 .
.
2.18. 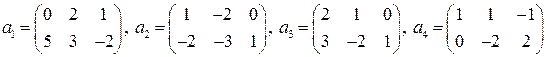 .
.
2.19.  ,
, 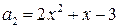 ,
,  ,
,
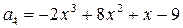 .
.
2.20.  ,
, 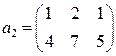 ,
, 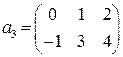 ,
,  .
.

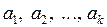 линейного пространства
линейного пространства  называется линейно зависимой, если существуют числа
называется линейно зависимой, если существуют числа  , среди которых есть хотя бы одно отличное от нуля, причем выполняется равенство
, среди которых есть хотя бы одно отличное от нуля, причем выполняется равенство . (1.1)
. (1.1) есть линейная комбинация остальных векторов:
есть линейная комбинация остальных векторов: .
. . В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы.
. В случае линейной зависимости выразить какой-нибудь вектор через остальные векторы системы. ,
,  ,
,  ,
, 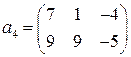 .
.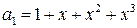 ,
,  ,
, 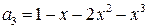 ,
, .
. ,
, 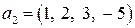 ,
, 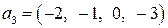 ,
, .
. ,
,  ,
,  ,
,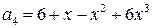 .
. ,
,  ,
,  ,
,  .
. (3, –4, 1, 2),
(3, –4, 1, 2),  (1, –1, –1, –1),
(1, –1, –1, –1), 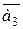 (4, –3, 1, 2),
(4, –3, 1, 2), 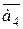 (1, –6, 1, 2).
(1, –6, 1, 2). ,
,  ,
, 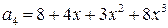 .
.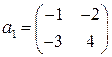 ,
,  ,
,  ,
,  .
. ,
, 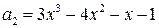 ,
,  ,
,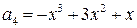 .
. .
. ,
,  ,
,  ,
,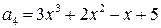 .
. ,
,  ,
,  ,
,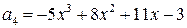 .
.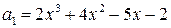 ,
, 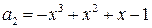 ,
,  ,
,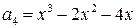 .
. ,
,  ,
, 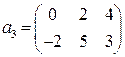 ,
, 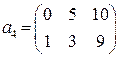 .
. ,
,  ,
,  ,
,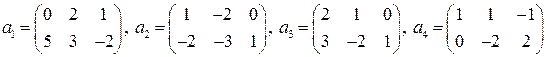 .
. ,
, 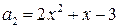 ,
,  ,
,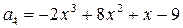 .
. ,
, 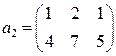 ,
, 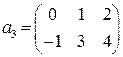 ,
,  .
.


