Образом  линейного оператора
линейного оператора  называется множество всех векторов
называется множество всех векторов 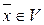 , для каждого из которых существует вектор
, для каждого из которых существует вектор  такой, что
такой, что 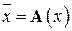 . Образ
. Образ  есть подпространство пространства V. Рангом
есть подпространство пространства V. Рангом  линейного оператора
линейного оператора 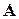 называется размерность образа
называется размерность образа  этого оператора.
этого оператора.
Ядром 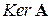 линейного оператора
линейного оператора  называется множество всех векторов
называется множество всех векторов 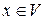 , которые переводятся в нулевой вектор
, которые переводятся в нулевой вектор 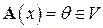 :
:
 .
.
Ядро 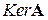 есть подпространство пространства V. Дефектом
есть подпространство пространства V. Дефектом 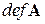 линейного оператора
линейного оператора 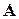 называется размерность ядра
называется размерность ядра 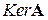 этого оператора.
этого оператора.
Справедливо равенство 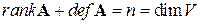 .
.
Подпространство  составлено из образов
составлено из образов 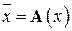 . Столбцами матрицы А являются координаты векторов
. Столбцами матрицы А являются координаты векторов  . Число линейно независимых столбцов матрицы А есть ранг матрицы, то есть ранг оператора
. Число линейно независимых столбцов матрицы А есть ранг матрицы, то есть ранг оператора  равен рангу матрицы А этого оператора:
равен рангу матрицы А этого оператора: 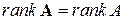 .
.
Задание 12. Выяснить, являются ли следующие преобразования  линейными операторами. Если являются, то описать их структуру (найти матрицу оператора, образ, ранг, ядро, дефект). Имеет ли оператор
линейными операторами. Если являются, то описать их структуру (найти матрицу оператора, образ, ранг, ядро, дефект). Имеет ли оператор  обратный оператор. Если имеет, то найти матрицу обратного оператора.
обратный оператор. Если имеет, то найти матрицу обратного оператора.
12.1. Преобразование  – замена каждого вектора
– замена каждого вектора  геометрического пространства
геометрического пространства 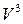 его зеркальным отображением относительно плоскости
его зеркальным отображением относительно плоскости 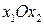 .
.
12.2. Дано линейное пространство векторов 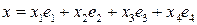 . Преобразование
. Преобразование  состоит в том, что у каждого вектора меняются местами вторая и третья координаты, а первая и четвертая координаты изменяют знак, то есть
состоит в том, что у каждого вектора меняются местами вторая и третья координаты, а первая и четвертая координаты изменяют знак, то есть 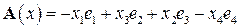 .
.
12.3. Пространство 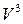 геометрических векторов
геометрических векторов  . Вводится преобразование
. Вводится преобразование 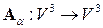 , заключающееся в проектировании вектора
, заключающееся в проектировании вектора  на плоскость
на плоскость 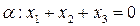 .
.
Указание к решению задачи: Преобразование 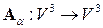 проектирования вектора
проектирования вектора  на плоскость
на плоскость 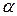 определяется равенством
определяется равенством 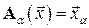 , где
, где 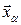 – ортогональная проекция вектора
– ортогональная проекция вектора  на плоскость
на плоскость 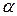 , причем
, причем  ,
, 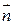 – нормальный вектор
– нормальный вектор 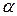 .
.
12.4.  – пространство многочленов
– пространство многочленов 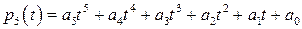 степеней, не превосходящих 5. Преобразование
степеней, не превосходящих 5. Преобразование 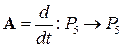 – операция дифференцирования:
– операция дифференцирования: 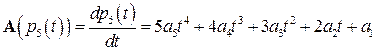 .
.
12.5. 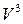 – пространство геометрических векторов
– пространство геометрических векторов  . Вводится преобразование
. Вводится преобразование 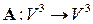 , действующее по правилу векторного произведения
, действующее по правилу векторного произведения
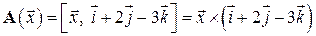 .
.
12.6. Является ли линейным оператором замена каждого геометрического вектора пространства  его зеркальным отображением относительно координатной плоскости
его зеркальным отображением относительно координатной плоскости  и увеличением вдвое второй координаты.
и увеличением вдвое второй координаты.
12.7. Дано линейное пространство векторов 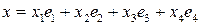 . Преобразование
. Преобразование  состоит в том, что у каждого вектора меняются местами первая и четвертая координаты, а вторая и третья координаты увеличиваются втрое
состоит в том, что у каждого вектора меняются местами первая и четвертая координаты, а вторая и третья координаты увеличиваются втрое  .
.
12.8. 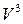 – пространство геометрических векторов
– пространство геометрических векторов  . Преобразование
. Преобразование 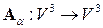 , заключающееся в проектировании вектора
, заключающееся в проектировании вектора  на плоскость
на плоскость 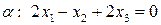 . Указание к решению задачи см. 12.3.
. Указание к решению задачи см. 12.3.
12.9. 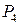 – пространство многочленов
– пространство многочленов 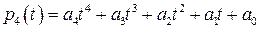 степеней, не превосходящих 4. Преобразование
степеней, не превосходящих 4. Преобразование 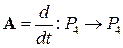 – операция дифференцирования:
– операция дифференцирования: 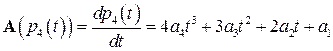 .
.
12.10. Пусть  – пространство геометрических векторов. Вводится преобразование
– пространство геометрических векторов. Вводится преобразование 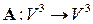 , действующее по правилу векторного произведения векторов:
, действующее по правилу векторного произведения векторов: 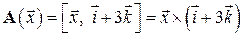 .
.
12.11. Является ли линейным оператором замена каждого геометрического вектора пространства  его зеркальным отображением относительно плоскости
его зеркальным отображением относительно плоскости 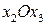 и увеличением втрое его первой координаты.
и увеличением втрое его первой координаты.
12.12. Дано линейное пространство векторов 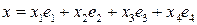 . Преобразование
. Преобразование  состоит в том, что у каждого вектора меняются местами первая и третья координаты, а вторая координата увеличивается вдвое, то есть
состоит в том, что у каждого вектора меняются местами первая и третья координаты, а вторая координата увеличивается вдвое, то есть 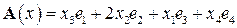 .
.
12.13. Пусть  – пространство геометрических векторов. Преобразование
– пространство геометрических векторов. Преобразование 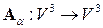 – проектирование вектора
– проектирование вектора  на плоскость
на плоскость 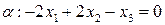 . Указание к решению задачи см. 12. 3.
. Указание к решению задачи см. 12. 3.
12.14. Пусть  – пространство геометрических векторов. Вводится преобразование
– пространство геометрических векторов. Вводится преобразование 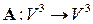 , действующее по правилу векторного произведения векторов
, действующее по правилу векторного произведения векторов 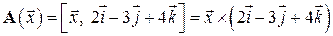 .
.
12.15. Пусть 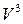 – пространство геометрических векторов
– пространство геометрических векторов  . Вводится преобразование
. Вводится преобразование 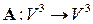 , действующее по правилу векторного произведения
, действующее по правилу векторного произведения 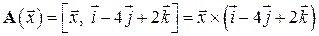 .
.
12.16. Пусть  – пространство геометрических векторов. Преобразование
– пространство геометрических векторов. Преобразование 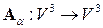 – проектирование вектора
– проектирование вектора  на плоскость
на плоскость  . Указание к решению задачи см. 12. 3.
. Указание к решению задачи см. 12. 3.
12.17.  – пространство геометрических векторов
– пространство геометрических векторов  . Преобразование
. Преобразование 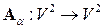 , заключающееся в повороте каждого вектора
, заключающееся в повороте каждого вектора  на некоторый постоянный угол
на некоторый постоянный угол  против часовой стрелки.
против часовой стрелки.
12.18.  – пространство геометрических векторов. Преобразование
– пространство геометрических векторов. Преобразование  , действующее по правилу векторного произведения векторов
, действующее по правилу векторного произведения векторов 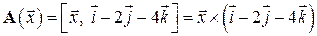 .
.
12.19. Пусть  – пространство геометрических векторов. Преобразование
– пространство геометрических векторов. Преобразование 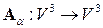 – проектирование вектора
– проектирование вектора 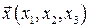 на плоскость
на плоскость  . Указание к решению задачи см. 12. 3.
. Указание к решению задачи см. 12. 3.
12.20. Пусть 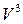 – пространство геометрических векторов
– пространство геометрических векторов 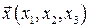 . Вводится преобразование
. Вводится преобразование  , действующее по правилу векторного произведения
, действующее по правилу векторного произведения 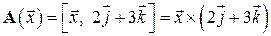 .
.
Задание 13. Выяснить, является ли отображение  , переводящее вектор
, переводящее вектор 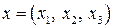 в вектор
в вектор 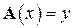 , линейным оператором. Если является, то найти матрицу этого оператора в стандартном базисе
, линейным оператором. Если является, то найти матрицу этого оператора в стандартном базисе  :
:  ,
, 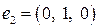 ,
,  линейного пространства
линейного пространства 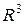 . Описать его структуру (найти образ, ранг, ядро, дефект).
. Описать его структуру (найти образ, ранг, ядро, дефект).
| 13.1.
| 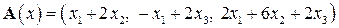 . .
|
| 13.2.
| 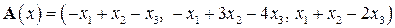 . .
|
| 13.3.
| 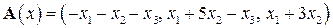 . .
|
| 13.4.
|  . .
|
| 13.5.
| 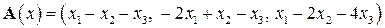 . .
|
| 13.6.
| 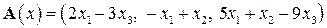 . .
|
| 13.7.
|  . .
|
| 13.8.
|  . .
|
| 13.9.
| 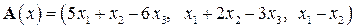 . .
|
| 13.10.
|  . .
|
| 13.11.
| 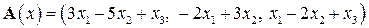 . .
|
| 13.12.
| 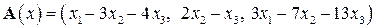 . .
|
| 13.13.
| 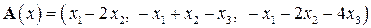 . .
|
| 13.14.
| 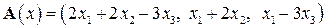 . .
|
| 13.15.
| 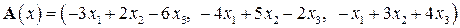 . .
|
| 13.16.
| 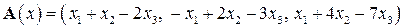 . .
|
| 13.17.
|  . .
|
| 13.18.
|  . .
|
| 13.19.
|  . .
|
| 13.20.
| 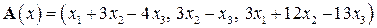 . .
|

 линейного оператора
линейного оператора  называется множество всех векторов
называется множество всех векторов 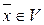 , для каждого из которых существует вектор
, для каждого из которых существует вектор  такой, что
такой, что 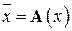 . Образ
. Образ  линейного оператора
линейного оператора 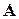 называется размерность образа
называется размерность образа 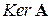 линейного оператора
линейного оператора 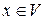 , которые переводятся в нулевой вектор
, которые переводятся в нулевой вектор 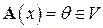 :
: .
.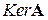 есть подпространство пространства V. Дефектом
есть подпространство пространства V. Дефектом 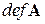 линейного оператора
линейного оператора 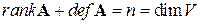 .
. . Число линейно независимых столбцов матрицы А есть ранг матрицы, то есть ранг оператора
. Число линейно независимых столбцов матрицы А есть ранг матрицы, то есть ранг оператора 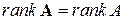 .
. геометрического пространства
геометрического пространства 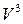 его зеркальным отображением относительно плоскости
его зеркальным отображением относительно плоскости 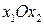 .
.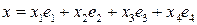 . Преобразование
. Преобразование 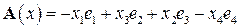 .
.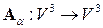 , заключающееся в проектировании вектора
, заключающееся в проектировании вектора 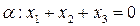 .
.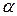 определяется равенством
определяется равенством 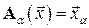 , где
, где 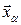 – ортогональная проекция вектора
– ортогональная проекция вектора  ,
, 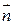 – нормальный вектор
– нормальный вектор  – пространство многочленов
– пространство многочленов 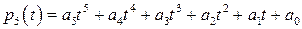 степеней, не превосходящих 5. Преобразование
степеней, не превосходящих 5. Преобразование 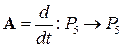 – операция дифференцирования:
– операция дифференцирования: 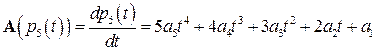 .
.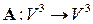 , действующее по правилу векторного произведения
, действующее по правилу векторного произведения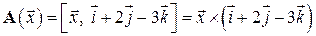 .
. его зеркальным отображением относительно координатной плоскости
его зеркальным отображением относительно координатной плоскости  и увеличением вдвое второй координаты.
и увеличением вдвое второй координаты.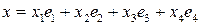 . Преобразование
. Преобразование  .
.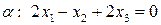 . Указание к решению задачи см. 12.3.
. Указание к решению задачи см. 12.3.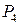 – пространство многочленов
– пространство многочленов 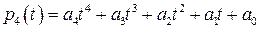 степеней, не превосходящих 4. Преобразование
степеней, не превосходящих 4. Преобразование 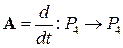 – операция дифференцирования:
– операция дифференцирования: 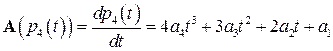 .
.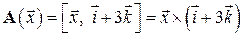 .
.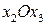 и увеличением втрое его первой координаты.
и увеличением втрое его первой координаты.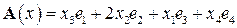 .
.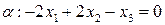 . Указание к решению задачи см. 12. 3.
. Указание к решению задачи см. 12. 3.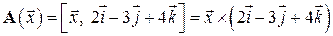 .
.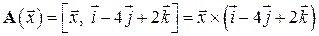 .
. . Указание к решению задачи см. 12. 3.
. Указание к решению задачи см. 12. 3. – пространство геометрических векторов
– пространство геометрических векторов  . Преобразование
. Преобразование  , заключающееся в повороте каждого вектора
, заключающееся в повороте каждого вектора  на некоторый постоянный угол
на некоторый постоянный угол  против часовой стрелки.
против часовой стрелки. – пространство геометрических векторов. Преобразование
– пространство геометрических векторов. Преобразование  , действующее по правилу векторного произведения векторов
, действующее по правилу векторного произведения векторов 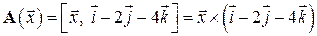 .
.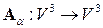 – проектирование вектора
– проектирование вектора 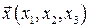 на плоскость
на плоскость  . Указание к решению задачи см. 12. 3.
. Указание к решению задачи см. 12. 3.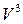 – пространство геометрических векторов
– пространство геометрических векторов 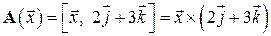 .
. , переводящее вектор
, переводящее вектор 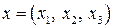 в вектор
в вектор 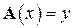 , линейным оператором. Если является, то найти матрицу этого оператора в стандартном базисе
, линейным оператором. Если является, то найти матрицу этого оператора в стандартном базисе  :
:  ,
, 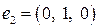 ,
,  линейного пространства
линейного пространства 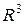 . Описать его структуру (найти образ, ранг, ядро, дефект).
. Описать его структуру (найти образ, ранг, ядро, дефект).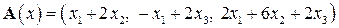 .
.
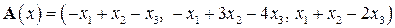 .
.
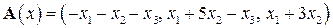 .
.
 .
.
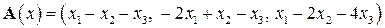 .
.
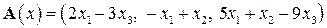 .
.
 .
.
 .
.
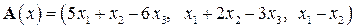 .
.
 .
.
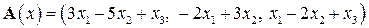 .
.
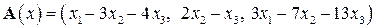 .
.
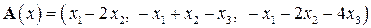 .
.
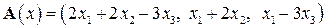 .
.
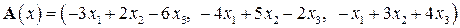 .
.
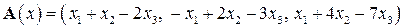 .
.
 .
.
 .
.
 .
.
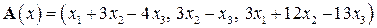 .
.



