Теорема Фредгольма, ее применение к исследованию СЛАУ
Рассмотрим неоднородную систему линейных алгебраических уравнений
где Система уравнений вида
где Теорема Фредгольма. Для того чтобы система (2.5) была совместной, необходимо и достаточно, чтобы вектор-столбец Задание 17 (применение теоремы Фредгольма к исследованию СЛАУ). Используя теорему Фредгольма, исследовать систему
на совместность. В ответе записать общее решение исходной СЛАУ и сопряженной СЛАУ. Фактические значения параметров
Задание 18 (применение теоремы Фредгольма к исследованию СЛАУ). Дана система (фактические значения параметров
1. Используя теорему Фредгольма, выяснить, при каком значении параметра 2. Провести исследование исходной системы, пользуясь теоремой Кронекера-Капелли. Показать, что СЛАУ будет совместна при найденном в пункте 1 значении параметра
|

 , (2.5)
, (2.5)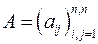 ,
, 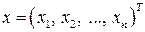 ,
,  .
.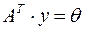 , (2.6)
, (2.6) ,
, 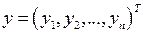 ,
,  называется однородной системой линейных алгебраических уравнений, сопряженной к системе (2.5).
называется однородной системой линейных алгебраических уравнений, сопряженной к системе (2.5). был ортогонален ко всем решениям
был ортогонален ко всем решениям 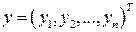 сопряженной системы (2.6).
сопряженной системы (2.6).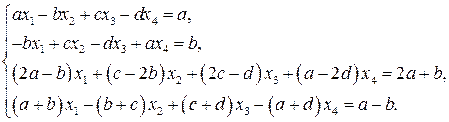
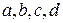 для соответствующего варианта взять из следующей таблицы:
для соответствующего варианта взять из следующей таблицы: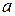
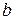

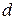

 система совместна.
система совместна.


