Ортогональные матрицы и ортогональные операторыКвадратная матрица Ортогональная матрица Линейный оператор Свойства ортогональных операторов: 1) ортогональный оператор сохраняет скалярное произведение векторов в евклидовом пространстве; 2) если 3) линейный оператор 4) линейный оператор является ортогональным тогда и только тогда, когда матрица оператора в ортонормированном базисе является ортогональной; 5) в евклидовом пространстве матрица перехода от одного ортонормированного базиса к другому ортонормированному базису является ортогональной; 6) если
где
|
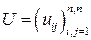называется ортогональной, если она удовлетворяет равенству 
.
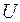обладает свойствами: 1) 
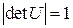; 2) 
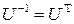; 3) матрицы 
, 
являются ортогональными матрицами.
в евклидовом пространстве V называется ортогональным, если для любых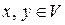 
: 
.
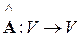– ортогональный оператор, 
– ортонормированный базис в V, то система векторов 
, 
, …., 
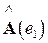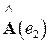– ортонормированный базис в V;
, переводящий ортонормированный базис 
в ортонормированный базис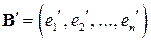 
: 
является ортогональным оператором;
и 
– матрицы ортогонального оператора 
в ортогональных базисах 
и 
, то они связаны равенством
,
– ортогональная матрица перехода от базиса 
