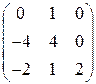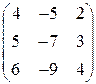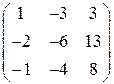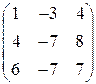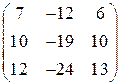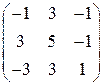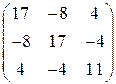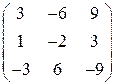Приведение матрицы линейного оператора к диагональному виду
Чтобы привести матрицу
Матрицу При этом имеет место равенство (2.7), где матрица
Задание 19. Выяснить, можно ли матрицу привести к диагональному виду переходом к новому базису. Если это можно сделать, то найти новый базис и соответствующее линейное преобразование.
Тема №3. Квадратичные формы Теоретические вопросы темы 1. Квадратичные формы, их матрицы, координатная и матричная формы записи. Ранг квадратичной формы. 2. Канонический вид квадратичной формы. Метод Лагранжа приведения квадратичной формы к каноническому виду. 3. Метод ортогональных преобразований для приведения квадратичной формы к каноническому виду. 4. Знакоопределенные и знакопеременные квадратичные формы, необходимые и достаточные условия. Критерий Сильвестра. Закон инерции. 5. Преобразование кривых 2-го порядка к каноническому виду ортогональным преобразованием.
|

 линейного оператора
линейного оператора  к диагональному виду необходимо, чтобы базис
к диагональному виду необходимо, чтобы базис 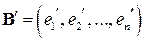 , в котором эта матрица является диагональной, состоял только из собственных векторов этой матрицы. Замена матрицы
, в котором эта матрица является диагональной, состоял только из собственных векторов этой матрицы. Замена матрицы 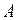 ей диагональной
ей диагональной  называется приведением матрицы к диагональному виду. Эта замена состоит в нахождении невырожденной матрицы
называется приведением матрицы к диагональному виду. Эта замена состоит в нахождении невырожденной матрицы  такой, что выполняется равенство
такой, что выполняется равенство  или
или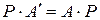 . (2.7)
. (2.7) можно привести к диагональному виду в том и только в том случае, если сумма размерностей всех собственных подпространств оператора равна размерности
можно привести к диагональному виду в том и только в том случае, если сумма размерностей всех собственных подпространств оператора равна размерности 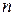 линейного пространства, в котором рассматривается этот оператор.
линейного пространства, в котором рассматривается этот оператор. ,
, – собственные значения матрицы
– собственные значения матрицы