Квадратичной формой 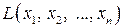 от n -переменных
от n -переменных  называется сумма следующего вида
называется сумма следующего вида
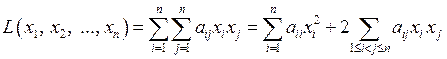 . (3.1)
. (3.1)
Запись вида (3.1) называется координатной формой записи квадратичной формы. Симметрическая матрица 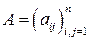 (
(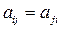 при всех
при всех 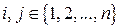 ) называется матрицей квадратичной формы.
) называется матрицей квадратичной формы.
Если обозначить векторы 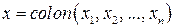 ,
, 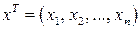 , то квадратичную форму (3.1) можно представить в виде
, то квадратичную форму (3.1) можно представить в виде
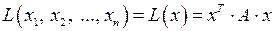 . (3.2)
. (3.2)
Запись вида (3.2) называется матричной формой записи квадратичной формы (3.1). Рангом квадратичной формы (3.1) называется ранг ее матрицы. Форма называется невырожденной (вырожденной), если матрица этой формы является невырожденной (вырожденной) матрицей.
Если имеется некоторое невырожденное линейное преобразование
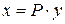 , (3.3)
, (3.3)
где 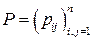 – невырожденная матрица,
– невырожденная матрица, 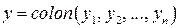 , то квадратичная форма (3.2) примет вид
, то квадратичная форма (3.2) примет вид
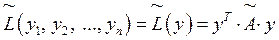 ,
, 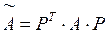 . (3.4)
. (3.4)
Квадратичная форма называется канонической, если она не содержит парных произведений вида 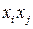 разных переменных, а содержит только квадраты переменных
разных переменных, а содержит только квадраты переменных 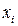 (
(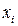 называются каноническими переменными):
называются каноническими переменными):
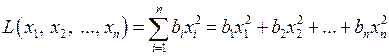 . (3.5)
. (3.5)
Любая квадратичная форма с помощью некоторого неособенного линейного преобразования может быть приведена к каноническому виду.
Метод Лагранжа (последовательного выделения полных квадратов) приведения квадратичной формы к каноническому виду состоит в следующем. Если 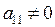 , то группируя слагаемые, содержащие переменную
, то группируя слагаемые, содержащие переменную 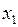 , получаем
, получаем
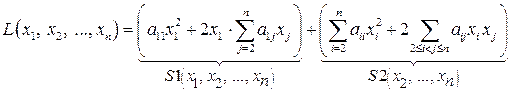 .
.
Выделяя полный квадрат по 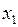 в сумме
в сумме 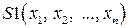 , имеем
, имеем
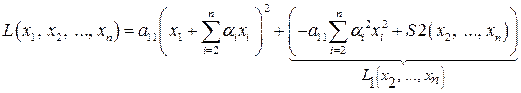 .
.
Обозначая 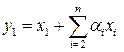 , получаем
, получаем
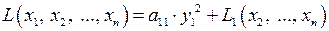 , (3.6)
, (3.6)
где 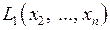 – квадратичная форма от (n –1)-переменных
– квадратичная форма от (n –1)-переменных 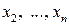 .
.
Выделяем в форме 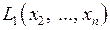 полный квадрат по переменной
полный квадрат по переменной 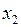 :
:
 ,
,
где 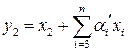 ,
, 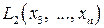 – квадратичная форма от (n –2)-переменных
– квадратичная форма от (n –2)-переменных 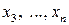 . И так далее. В результате такого алгоритма (последовательного выделения полных квадратов) получим канонический вид (3.5).
. И так далее. В результате такого алгоритма (последовательного выделения полных квадратов) получим канонический вид (3.5).
Задание 20. Привести квадратичную форму 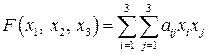 к каноническому виду
к каноническому виду 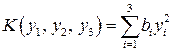 методом Лагранжа, указать соответствующее неособенное линейное преобразование. Сделать проверку.
методом Лагранжа, указать соответствующее неособенное линейное преобразование. Сделать проверку.
20.1. 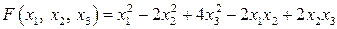 . .
|
20.2. 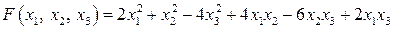 . .
|
20.3. 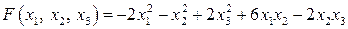 . .
|
20.4. 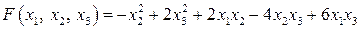 . .
|
20.5. 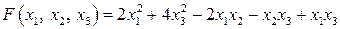 . .
|
20.6. 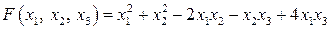 . .
|
20.7. 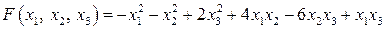 . .
|
20.8. 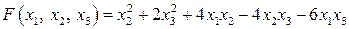 . .
|
20.9. 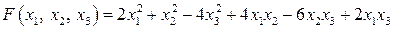 . .
|
20.10. 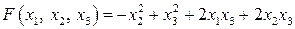 . .
|
20.11. 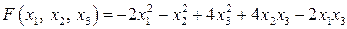 . .
|
20.12.  . .
|
20.13. 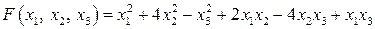 . .
|
20.14. 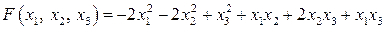 . .
|
20.15. 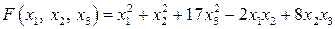 . .
|
20.16. 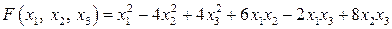 . .
|
20.17. 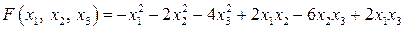 . .
|
20.18. 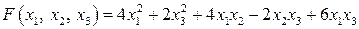 . .
|
20.19.  . .
|
20.20. 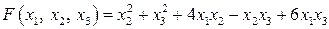 . .
|

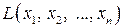 от n -переменных
от n -переменных  называется сумма следующего вида
называется сумма следующего вида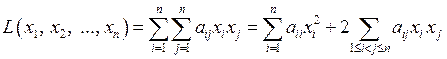 . (3.1)
. (3.1)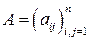 (
(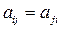 при всех
при всех 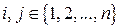 ) называется матрицей квадратичной формы.
) называется матрицей квадратичной формы.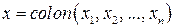 ,
, 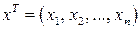 , то квадратичную форму (3.1) можно представить в виде
, то квадратичную форму (3.1) можно представить в виде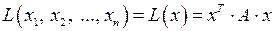 . (3.2)
. (3.2)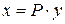 , (3.3)
, (3.3)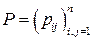 – невырожденная матрица,
– невырожденная матрица, 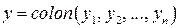 , то квадратичная форма (3.2) примет вид
, то квадратичная форма (3.2) примет вид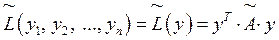 ,
, 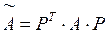 . (3.4)
. (3.4)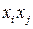 разных переменных, а содержит только квадраты переменных
разных переменных, а содержит только квадраты переменных 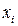 (
(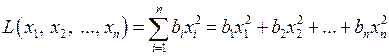 . (3.5)
. (3.5)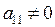 , то группируя слагаемые, содержащие переменную
, то группируя слагаемые, содержащие переменную 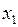 , получаем
, получаем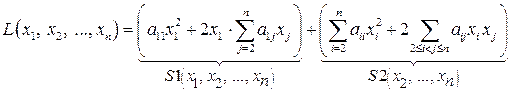 .
.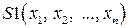 , имеем
, имеем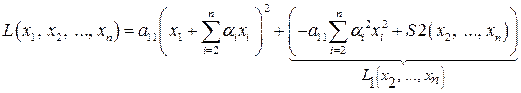 .
.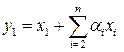 , получаем
, получаем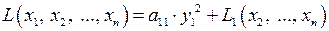 , (3.6)
, (3.6)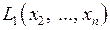 – квадратичная форма от (n –1)-переменных
– квадратичная форма от (n –1)-переменных 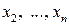 .
.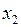 :
: ,
,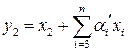 ,
, 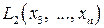 – квадратичная форма от (n –2)-переменных
– квадратичная форма от (n –2)-переменных 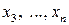 . И так далее. В результате такого алгоритма (последовательного выделения полных квадратов) получим канонический вид (3.5).
. И так далее. В результате такого алгоритма (последовательного выделения полных квадратов) получим канонический вид (3.5).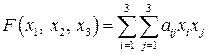 к каноническому виду
к каноническому виду 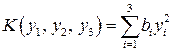 методом Лагранжа, указать соответствующее неособенное линейное преобразование. Сделать проверку.
методом Лагранжа, указать соответствующее неособенное линейное преобразование. Сделать проверку.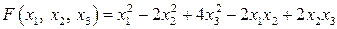 .
.
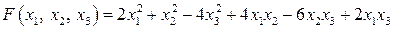 .
.
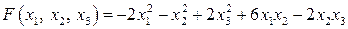 .
.
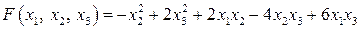 .
.
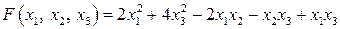 .
.
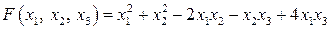 .
.
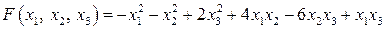 .
.
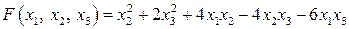 .
.
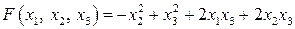 .
.
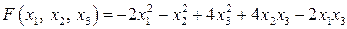 .
.
 .
.
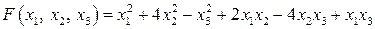 .
.
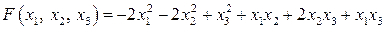 .
.
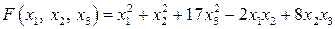 .
.
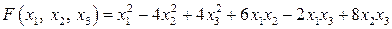 .
.
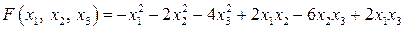 .
.
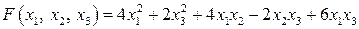 .
.
 .
.
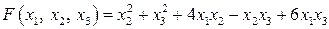 .
.



