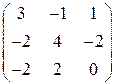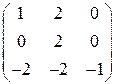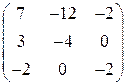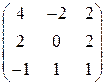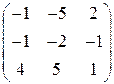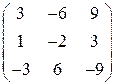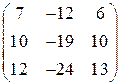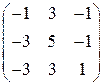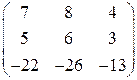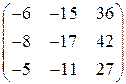Пусть  – линейный оператор. Ненулевой вектор
– линейный оператор. Ненулевой вектор  , удовлетворяющий условию (операторному равенству)
, удовлетворяющий условию (операторному равенству)
 ,
, 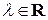 , (2.1)
, (2.1)
называется собственным вектором оператора  . Число
. Число 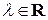 при этом называется собственным значением (собственным числом), соответствующим собственному вектору
при этом называется собственным значением (собственным числом), соответствующим собственному вектору  .
.
Говорят о собственных значениях и собственных векторах квадратной матрицы. При этом имеют в виду, что линейному оператору  соответствует матрица
соответствует матрица 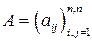 в фиксированном базисе пространства.
в фиксированном базисе пространства.
Операторное равенство (2.1) можно переписать в матричном виде
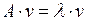 ,
, 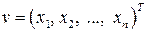 ,
,
( – координаты собственного вектора) или в виде системы уравнений
– координаты собственного вектора) или в виде системы уравнений
 (2.2)
(2.2)
Уравнение вида
 (2.3)
(2.3)
называется характеристическим уравнением оператора  (уравнением для нахождения собственных значений оператора). Разложив определитель
(уравнением для нахождения собственных значений оператора). Разложив определитель 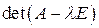 в уравнении (2.3), получим многочлен
в уравнении (2.3), получим многочлен
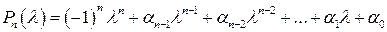 , (2.4)
, (2.4)
называемый характеристическим многочленом оператора  , его корни [решения уравнения (2.3)] – характеристическими корнями многочлена (2.4).
, его корни [решения уравнения (2.3)] – характеристическими корнями многочлена (2.4).
При каждом найденном из уравнения (2.3) собственном значении 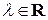 однородная система (2.2) будет иметь ненулевые решения. Выделив фундаментальную систему линейно независимых решений, получим либо единственный собственный вектор
однородная система (2.2) будет иметь ненулевые решения. Выделив фундаментальную систему линейно независимых решений, получим либо единственный собственный вектор  , либо систему r линейно независимых собственных векторов
, либо систему r линейно независимых собственных векторов 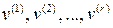 оператора
оператора  .
.
Число r линейно независимых собственных векторов, отвечающих одному собственному значению, называется геометрической кратностью собственного значения.
Алгебраической кратностью собственного значения 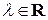 называется такое число
называется такое число 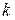 , что
, что 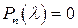 ,
,  , …,
, …,  ,
,  .
.
Если  – попарно различные собственные значения оператора
– попарно различные собственные значения оператора  , то система
, то система  соответствующих им собственных векторов линейно независима.
соответствующих им собственных векторов линейно независима.
Задание 15. Найти собственные числа и соответственные собственные векторы линейного оператора, заданного матрицей в некотором базисе.
| 15.1
| 
| 15.2
| 
| 15.3
| 
|
| 15.4
| 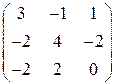
| 15.5
| 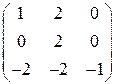
| 15.6
| 
|
| 15.7
| 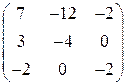
| 15.8
| 
| 15.9
| 
|
| 15.10
| 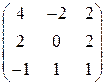
| 15.11
| 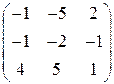
| 15.12
| 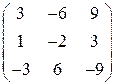
|
| 15.13
| 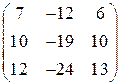
| 15.14
| 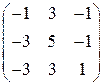
| 15.15
| 
|
| 15.16
| 
| 15.17
| 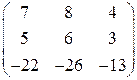
| 15.18
| 
|
| 15.19
| 
| 15.20
| 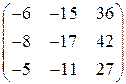
|
|
|

 – линейный оператор. Ненулевой вектор
– линейный оператор. Ненулевой вектор  , удовлетворяющий условию (операторному равенству)
, удовлетворяющий условию (операторному равенству) ,
, 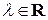 , (2.1)
, (2.1)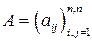 в фиксированном базисе пространства.
в фиксированном базисе пространства.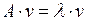 ,
, 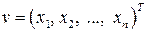 ,
, – координаты собственного вектора) или в виде системы уравнений
– координаты собственного вектора) или в виде системы уравнений (2.2)
(2.2) (2.3)
(2.3)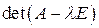 в уравнении (2.3), получим многочлен
в уравнении (2.3), получим многочлен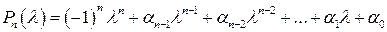 , (2.4)
, (2.4) , его корни [решения уравнения (2.3)] – характеристическими корнями многочлена (2.4).
, его корни [решения уравнения (2.3)] – характеристическими корнями многочлена (2.4). , либо систему r линейно независимых собственных векторов
, либо систему r линейно независимых собственных векторов 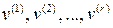 оператора
оператора 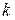 , что
, что 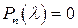 ,
,  , …,
, …,  ,
,  .
. – попарно различные собственные значения оператора
– попарно различные собственные значения оператора  соответствующих им собственных векторов линейно независима.
соответствующих им собственных векторов линейно независима.