Пусть в евклидовом пространстве  :
:
 ,
,  (1.7)
(1.7)
есть ортогональная система векторов: 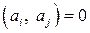 ,
,  ,
,  .
.
Систему векторов (1.7) можно дополнить до ортогонального базиса
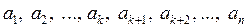 .
.
Вектор  подбирается так, чтобы он был ортогонален векторам
подбирается так, чтобы он был ортогонален векторам 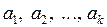 . При этом необходимо решить систему
. При этом необходимо решить систему
 ,
,  , …,
, …, 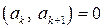 , (1.8)
, (1.8)
содержащую  -уравнений (
-уравнений ( ) с
) с  -неизвестными
-неизвестными 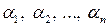 . Из общего решения этой системы необходимо выделить нетривиальное частное решение, которое определит координаты вектора
. Из общего решения этой системы необходимо выделить нетривиальное частное решение, которое определит координаты вектора 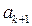 .
.
Вектор 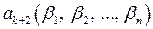 подбирается так, чтобы он был ортогонален векторам
подбирается так, чтобы он был ортогонален векторам  . При этом необходимо решить систему
. При этом необходимо решить систему
 ,
, 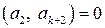 , …,
, …, 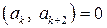 ,
,  . (1.9)
. (1.9)
Система (1.9) будет содержать ( +1)-уравнение (если
+1)-уравнение (если  ) с
) с  -неизвестными
-неизвестными 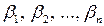 . Из общего решения этой системы необходимо выделить нетривиальное частное решение, определяющее координаты вектора
. Из общего решения этой системы необходимо выделить нетривиальное частное решение, определяющее координаты вектора  . И так далее. В итоге получим систему ортогональных векторов
. И так далее. В итоге получим систему ортогональных векторов
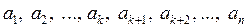 ,
,
являющуюся ортогональным базисом в пространстве  .
.
Задание 9. Проверить ортогональность векторов  ,
, 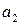 пространства
пространства 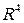 и дополнить эти векторы до ортогонального базиса.
и дополнить эти векторы до ортогонального базиса.
9.1. 
9.2. 
9.3. 
9.4. 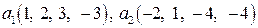
9.5. 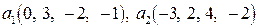
9.6. 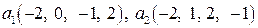
9.7. 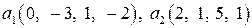
9.8. 
9.9. 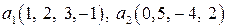
9.10. 
9.11. 
9.12. 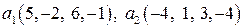
9.13. 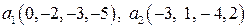
9.14. 
9.15. 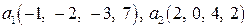
9.16. 
9.17. 
9.18. 
9.19. 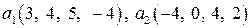
9.20. 
Задание 10. Подпространство 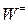 линейного пространства
линейного пространства 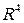 задано однородной системой линейных алгебраических уравнений (ОСЛАУ). Найти ортогональную проекцию
задано однородной системой линейных алгебраических уравнений (ОСЛАУ). Найти ортогональную проекцию  вектора
вектора 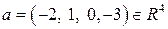 на подпространство
на подпространство 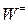 и его ортогональную составляющую
и его ортогональную составляющую  .
.
Алгоритм решения задания следующий.
1. Находим общее решение ОСЛАУ и фундаментальную систему решений  (базис пространства решений ОСЛАУ).
(базис пространства решений ОСЛАУ).
2. Проверяем ортогональность векторов  . Если векторы не ортогональны, то проводим процесс ортогонализации Шмидта, получаем систему ортонормированных векторов
. Если векторы не ортогональны, то проводим процесс ортогонализации Шмидта, получаем систему ортонормированных векторов  :
:
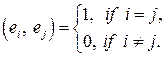
3. Ортогональную проекцию – вектор  составляем по правилу
составляем по правилу
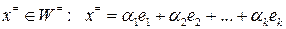 ,
,
где  ,
, 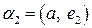 , ….,
, …., 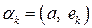 . Проверяем принадлежность составленного вектора
. Проверяем принадлежность составленного вектора 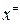 пространству
пространству 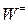 .
.
4. Ортогональную составляющую – вектор  составляем как
составляем как
 .
.
Ортогональность векторов  ,
,  проверяем условием
проверяем условием  .
.
10.1. 
| 10.2. 
|
10.3. 
| 10.4. 
|
10.5. 
| 10.6. 
|
10.7. 
| 10.8. 
|
10.9. 
| 10.10. 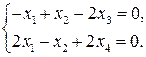
|
10.11. 
| 10.12. 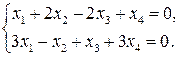
|
10.13. 
| 10.14. 
|
10.15. 
| 10.16. 
|
10.17. 
| 10.18. 
|
10.19. 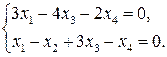
| 10.20. 
|
Задание 11. Найти базис  ортогонального дополнения линейного подпространства
ортогонального дополнения линейного подпространства 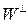 для соответствующего линейного подпространства
для соответствующего линейного подпространства 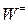 решений ОСЛАУ задания 3. Написать ОСЛАУ, соответствующую подпространству
решений ОСЛАУ задания 3. Написать ОСЛАУ, соответствующую подпространству 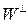 .
.

 :
: ,
,  (1.7)
(1.7)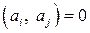 ,
,  ,
,  .
.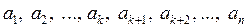 .
. подбирается так, чтобы он был ортогонален векторам
подбирается так, чтобы он был ортогонален векторам 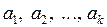 . При этом необходимо решить систему
. При этом необходимо решить систему ,
,  , …,
, …, 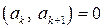 , (1.8)
, (1.8) -уравнений (
-уравнений ( -неизвестными
-неизвестными 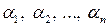 . Из общего решения этой системы необходимо выделить нетривиальное частное решение, которое определит координаты вектора
. Из общего решения этой системы необходимо выделить нетривиальное частное решение, которое определит координаты вектора 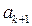 .
.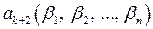 подбирается так, чтобы он был ортогонален векторам
подбирается так, чтобы он был ортогонален векторам  . При этом необходимо решить систему
. При этом необходимо решить систему ,
, 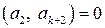 , …,
, …, 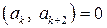 ,
,  . (1.9)
. (1.9) ) с
) с 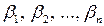 . Из общего решения этой системы необходимо выделить нетривиальное частное решение, определяющее координаты вектора
. Из общего решения этой системы необходимо выделить нетривиальное частное решение, определяющее координаты вектора  . И так далее. В итоге получим систему ортогональных векторов
. И так далее. В итоге получим систему ортогональных векторов ,
, 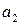 пространства
пространства 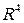 и дополнить эти векторы до ортогонального базиса.
и дополнить эти векторы до ортогонального базиса.


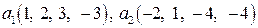
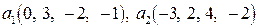
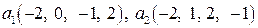
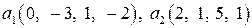

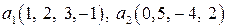


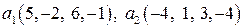
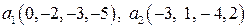

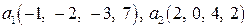



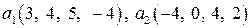

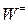 линейного пространства
линейного пространства  вектора
вектора 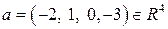 на подпространство
на подпространство  .
. (базис пространства решений ОСЛАУ).
(базис пространства решений ОСЛАУ). :
: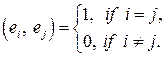
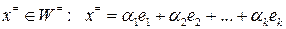 ,
, ,
, 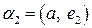 , ….,
, …., 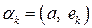 . Проверяем принадлежность составленного вектора
. Проверяем принадлежность составленного вектора 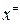 пространству
пространству  .
. .
.








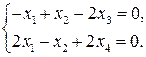

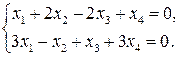






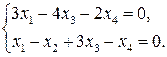

 ортогонального дополнения линейного подпространства
ортогонального дополнения линейного подпространства 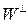 для соответствующего линейного подпространства
для соответствующего линейного подпространства 


