Система векторов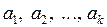 
евклидова пространства 
со скалярным произведением 
(
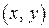) называется ортогональной, если эти векторы взаимно ортогональны [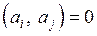 
при всех 
, 
]. Ортогональная система векторов линейно независима.
В евклидовом пространстве размерности 
существует ортонормированный базис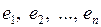 
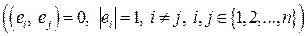. Этот базис можно построить по линейно независимой системе векторов 
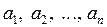с помощью процесса ортогонализации Шмидта:
 ;
|  ,  ;
|
 ;
|  ,  ,  ;
|
 ;
|  ,  ,  ,
 ;
|
| ………………………………………
| …………………………..
|
|  ,  ,  ,
 , …  .
|
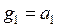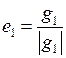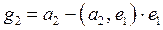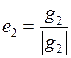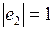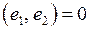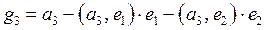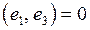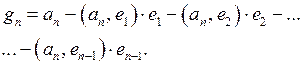
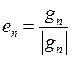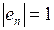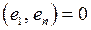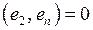Задание 8. Доказать, что система векторов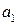 
, 
, 
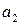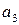пространства 
является базисом. Построить по этой системе ортонормированный базис (провести процесс ортогонализации Шмидта).
| 8.1.
|  .
|
| 8.2.
|  .
|
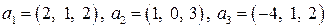| 8.3.
|  .
|
| 8.4.
|  .
|
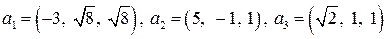| 8.5.
|  .
|
| 8.6.
|  .
|
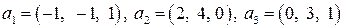| 8.7.
|  .
|
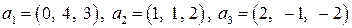| 8.8.
|  .
|
| 8.9.
|  .
|
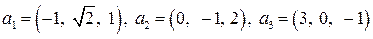| 8.10.
|  .
|
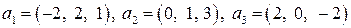| 8.11.
|  .
|
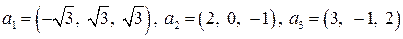| 8.12.
|  .
|
| 8.13.
|  .
|
| 8.14.
|  .
|
| 8.15.
|  .
|
| 8.16.
|  .
|
| 8.17.
|  .
|
| 8.18.
|  .
|
| 8.19.
|  .
|
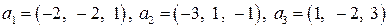| 8.20.
|  .
|
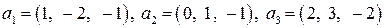