Пусть V – евклидово пространство с ортонормированным базисом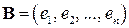 
. Линейный оператор 
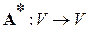называется сопряженным к оператору 
, если для любых 
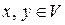выполняется равенство:
.
Любому линейному оператору 
соответствует единственный сопряженный оператор 
, причем его матрицей 
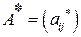является матрица, транспонированная к матрице 
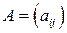линейного оператора .
Задание 16. Линейный оператор 
в базисе 
имеет матрицу 
(
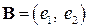– ортонормированный базис). Найти матрицу 
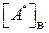сопряженного линейного оператора 
в базисе . Проверить справедливость равенства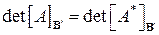 
.
16.1.  , 
| 16.2.  ,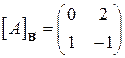 
|
16.3.  , 
| 16.4.  ,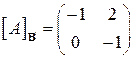 
|
16.5.  ,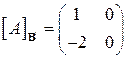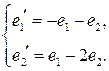 
| 16.6.  ,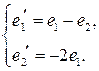 
|
16.7.  ,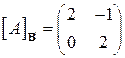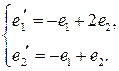 
| 16.8.  ,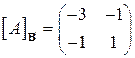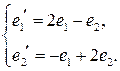 
|
16.9.  ,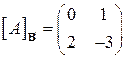 
| 16.10.  ,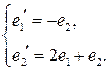 
|
16.11.  , 
| 16.12.  , 
|
16.13.  ,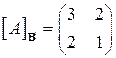 
| 16.14.  ,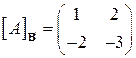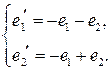 
|
16.15.  ,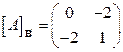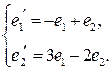 
| 16.16.  ,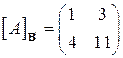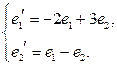 
|
16.17.  ,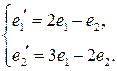 
| 16.18.  ,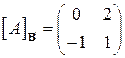 
|
16.19. ,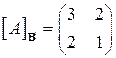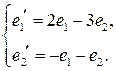 
| 16.20.  ,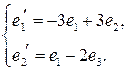 
|
