Построение проектируемой зубчатой передачи
1) Откладываем межосевое расстояние аw и проводим окружности dw1 dw2 делительные d1, d2, и основные db1, db2, окружности вершин dа1, dа2, и впадин df1, df2, Начальные окружности касаются в полюсе зацепления. Расстояние между делительными окружностями по осевой линии равно ym. Расстояние между окружностями вершин одного колеса и окружностями впадин другого, измеренное по оси, равно С*m. 2) Через полюс зацепления касательной к основным окружностям колес проводим линию зацепления. В точке касания N1 и N2 называются предельными точками линии зацепления. Буквами В1 и В2 отмечена активная линия зацепления,точка В1 – точка начала зацепления, точка В2 - точка конца зацепления. Зубья шестерни копируем из построения станочного зацепления, а зубья зубчатого колеса получаем графическим построением.
Расчет планетарного редуктора
Исходные данные: Передаточное отношение планетарного редуктора: u1H= nd * z5 / (n1 * z6) = 2920*12/(100 *23) = 15.23 Число сателлитов K=3; Структурная схема: двухрядный планетарный механизм с одним внутренним и одним внешним зацеплением. Расчетное передаточное отношение должно отличаться от заданного не больше, чем на ±5%. Передаточное отношение принимаем равное 15. По теореме Виллиса передаточное отношение двухрядного планетарного редуктора с одним внутренним и одним внешним зацеплениями:
Для определения чисел зубьев колес данного редуктора воспользуемся методом сомножителей. Из условия передаточного отношения определяем числовое значение
1)принимем, что A=1, B=2, C=2, D=14. Из условия соосности
2)принимем, что A=1, B=2, C=2, D=14:
3)принимем, что A=1, B=3, C=3, D=14.
Из условия минимальности габаритов принимаем второй вариант. Условие сборки:
Условие соседства:
Проверим, выполняется ли условие отсутствия подрезания:
Значит, выбранные числа зубьев колес удовлетворяют всем требованиям.
|


 , и полученное число раскладываем на сомножители А, В, С, D, которым числа зубьев z1,z2,z3,z4, должны быть соответственно пропорциональны. Чтобы обеспечить соосность механизма, вводят дополнительные множители.
, и полученное число раскладываем на сомножители А, В, С, D, которым числа зубьев z1,z2,z3,z4, должны быть соответственно пропорциональны. Чтобы обеспечить соосность механизма, вводят дополнительные множители. ;
; определяем числа зубьев:
определяем числа зубьев:





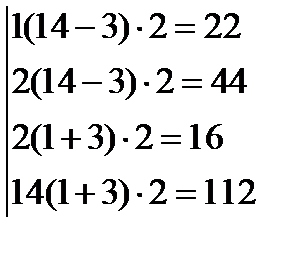

 -можно подобрать числа;
-можно подобрать числа;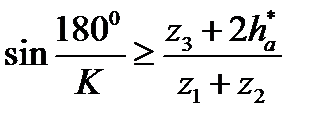
 -условие соседства выполняется;
-условие соседства выполняется; для колес с внешним зацеплением;
для колес с внешним зацеплением; для колес с внутренним зацеплением.
для колес с внутренним зацеплением. , значит условие выполняется.
, значит условие выполняется.


